题目内容
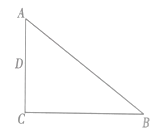
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点.
边的中点.
(1)尺规作图:作出以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
(2)求证:![]() 是圆
是圆![]() 的切线.
的切线.
(3)当![]() 时,四边形
时,四边形![]() 是平行四边形,此时,四边形
是平行四边形,此时,四边形![]() 的形状为 .
的形状为 .
【答案】(1)见解析;(2)见解析;(3)![]() ,正方形
,正方形
【解析】
(1)先做出线段BC的垂直平分线线,确定圆心O,然后以OB为半径画圆即可;
(2)由BC为直径,D为AC的中点得到OD∥AB,然后根据平行线的性质和全等三角形的判定和性质证明即可;
(3)根据平行四边形的判定和平行线的性质即可确定∠ABC的度数;先说明![]() 为菱形,再说明其为正方形即可.
为菱形,再说明其为正方形即可.
解:(1)如图
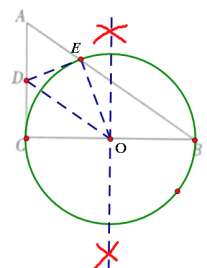 ;
;
(2)证明:如图:连接![]() ,
,
∵点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为圆心.
为圆心.
∴![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() 是圆
是圆![]() 的切线
的切线
(3)由(2)得![]() ,
,![]()
要使四边形![]() 是平行四边形,则DE∥OB
是平行四边形,则DE∥OB
∴∠AED=∠B
∴∠AED=∠OEB
又∵∠DEO=90°
∴当![]() 45°时,四边形
45°时,四边形![]() 是平行四边形
是平行四边形
∵![]()
∴∠AED=∠ODE=∠OEB=∠B
∴OE=DE
又∵![]()
∴CD=DE
∴CD=DE=OE=OC
∴四边形![]() 是菱形
是菱形
又∵∠OCD=90°
∴四边形![]() 是正方形
是正方形
故答案为:45°,正方形.

练习册系列答案
相关题目