题目内容
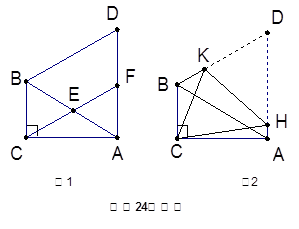
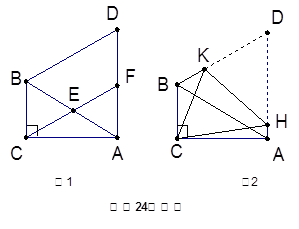
如图，C在AB的延长线上，CE⊥AF于E，交FB于D，若∠F=40°，∠C=20°，则∠FBA的度数为
- A.50°
- B.60°
- C.70°
- D.80°
C
分析：先根据三角形内角和定理求出∠EDF的度数，再根据对顶角的性质求出∠CDB的度数，由三角形外角的性质即可求出∠FBA的度数．
解答：∵CE⊥AF于E，∴∠FED=90°，
∵∠F=40°，
∴∠EDF=180°-∠FED-∠F=180°-90°-40°=50°，
∵∠EDF=∠CDB，
∴∠CDB=50°，
∵∠C=20°，∠FBA是△BDC的外角，
∴∠FBA=∠CDB+∠C=50°+20°=70°．
故选C．
点评：本题考查的是三角形内角和定理及外角的性质，解答此题的关键是熟知以下知识：
（1）三角形的内角和为180°；
（2）三角形的外角等于与之不相邻的两个内角的和．
分析：先根据三角形内角和定理求出∠EDF的度数，再根据对顶角的性质求出∠CDB的度数，由三角形外角的性质即可求出∠FBA的度数．
解答：∵CE⊥AF于E，∴∠FED=90°，
∵∠F=40°，
∴∠EDF=180°-∠FED-∠F=180°-90°-40°=50°，
∵∠EDF=∠CDB，
∴∠CDB=50°，
∵∠C=20°，∠FBA是△BDC的外角，
∴∠FBA=∠CDB+∠C=50°+20°=70°．
故选C．
点评：本题考查的是三角形内角和定理及外角的性质，解答此题的关键是熟知以下知识：
（1）三角形的内角和为180°；
（2）三角形的外角等于与之不相邻的两个内角的和．
练习册系列答案
相关题目
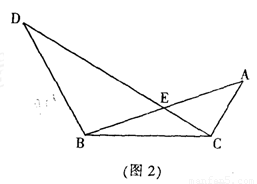
如图点D在△ABC的AB边上，AD=BD=CD=1，延长BC至E，BC=CE，连接AE，则AE=
