题目内容
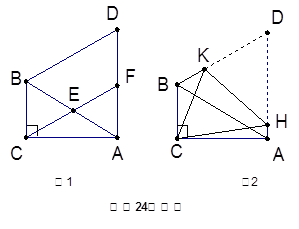
在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形【小题1】如图1, E是AB的中点,连结CE并延长交AD于F.
求证:① △AEF≌△BEC;
② 四边形BCFD是平行四边形;
【小题2】如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,求sin∠ACH的值.
C
【小题1】① 在△ABC中,∠ACB=90°,∠CAB=30°,
∴ ∠ABC=60°.
在等边△ABD中,∠BAD=60°, ∴ ∠BAD=∠ABC="60°" .
∵ E为AB的中点,∴ AE=BE.
又∵ ∠AEF=∠BEC , ∴ △AEF≌△BEC 3分
② 在△ABC中,∠ACB=90°,E为AB的中点
∴ CE= AB,BE=
AB,BE= AB, ∴ ∠BCE=∠EBC="60°" .
AB, ∴ ∠BCE=∠EBC="60°" .
又∵ △AEF≌△BEC, ∴ ∠AFE=∠BCE="60°" .
又∵ ∠D=60°, ∴ ∠AFE=∠D=60° ∴ FC∥BD
又∵ ∠BAD=∠ABC=60°,∴ AD∥BC,即FD∥BC
∴ 四边形BCFD是平行四边形.
【小题2】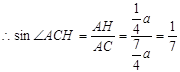 解析:
解析:
which引导非限制性定语从句,which常用作实意动词的主语。① 在△ABC中,∠ACB=90°,∠CAB=30°,
∴ ∠ABC=60°.
在等边△ABD中,∠BAD=60°, ∴ ∠BAD=∠ABC="60°" .
∵ E为AB的中点,∴ AE=BE.
又∵ ∠AEF=∠BEC , ∴ △AEF≌△BEC 3分
② 在△ABC中,∠ACB=90°,E为AB的中点
∴ CE= AB,BE=
AB,BE= AB, ∴ ∠BCE=∠EBC="60°" .
AB, ∴ ∠BCE=∠EBC="60°" .
又∵ △AEF≌△BEC, ∴ ∠AFE=∠BCE="60°" .
又∵ ∠D=60°, ∴ ∠AFE=∠D=60° ∴ FC∥BD
又∵ ∠BAD=∠ABC=60°,∴ AD∥BC,即FD∥BC
∴ 四边形BCFD是平行四边形.
(2)∵∠BAD=60°,∠CAB=30° ∴∠CAH=90°
在Rt△ABC中,∠CAB=30°,设BC =a
∴ AB=2BC=2a,∴ AD=AB=2a.
设AH =" x" ,则 HC=HD=AD-AH=2a-x.
在Rt△ABC中,AC2=(2a) 2-a2=3a2.
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a-x) 2.
解得 x=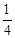 a,即AH=
a,即AH=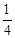 a.
a.
∴ HC=2a-x=2a-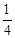 a=
a=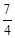 a
a
【小题1】① 在△ABC中,∠ACB=90°,∠CAB=30°,
∴ ∠ABC=60°.
在等边△ABD中,∠BAD=60°, ∴ ∠BAD=∠ABC="60°" .
∵ E为AB的中点,∴ AE=BE.
又∵ ∠AEF=∠BEC , ∴ △AEF≌△BEC 3分
② 在△ABC中,∠ACB=90°,E为AB的中点
∴ CE=
 AB,BE=
AB,BE= AB, ∴ ∠BCE=∠EBC="60°" .
AB, ∴ ∠BCE=∠EBC="60°" . 又∵ △AEF≌△BEC, ∴ ∠AFE=∠BCE="60°" .
又∵ ∠D=60°, ∴ ∠AFE=∠D=60° ∴ FC∥BD
又∵ ∠BAD=∠ABC=60°,∴ AD∥BC,即FD∥BC
∴ 四边形BCFD是平行四边形.
【小题2】
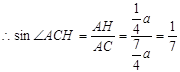 解析:
解析:which引导非限制性定语从句,which常用作实意动词的主语。① 在△ABC中,∠ACB=90°,∠CAB=30°,
∴ ∠ABC=60°.
在等边△ABD中,∠BAD=60°, ∴ ∠BAD=∠ABC="60°" .
∵ E为AB的中点,∴ AE=BE.
又∵ ∠AEF=∠BEC , ∴ △AEF≌△BEC 3分
② 在△ABC中,∠ACB=90°,E为AB的中点
∴ CE=
 AB,BE=
AB,BE= AB, ∴ ∠BCE=∠EBC="60°" .
AB, ∴ ∠BCE=∠EBC="60°" . 又∵ △AEF≌△BEC, ∴ ∠AFE=∠BCE="60°" .
又∵ ∠D=60°, ∴ ∠AFE=∠D=60° ∴ FC∥BD
又∵ ∠BAD=∠ABC=60°,∴ AD∥BC,即FD∥BC
∴ 四边形BCFD是平行四边形.
(2)∵∠BAD=60°,∠CAB=30° ∴∠CAH=90°
在Rt△ABC中,∠CAB=30°,设BC =a
∴ AB=2BC=2a,∴ AD=AB=2a.
设AH =" x" ,则 HC=HD=AD-AH=2a-x.
在Rt△ABC中,AC2=(2a) 2-a2=3a2.
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a-x) 2.
解得 x=
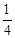 a,即AH=
a,即AH=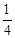 a.
a.∴ HC=2a-x=2a-
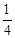 a=
a=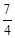 a
a 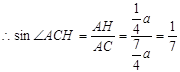

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=