题目内容
抛物线y=-x2和直线y=x-3交点的横坐标为
- A.x1=1，x2=-3
- B.x1=-1，x2=3
- C.
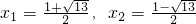
- D.
D
分析：令两函数值相等即可得到-x2=x-3，解方程即可求得两交点横坐标；
解答：根据题意得：-x2=x-3
解得：x1=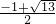
，x2=
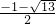
故选D．
点评：本题考查了二次函数的性质，求两个函数的交点坐标时，可以让两个函数的函数值相等．
分析：令两函数值相等即可得到-x2=x-3，解方程即可求得两交点横坐标；
解答：根据题意得：-x2=x-3
解得：x1=
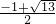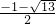
，x2=故选D．
点评：本题考查了二次函数的性质，求两个函数的交点坐标时，可以让两个函数的函数值相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
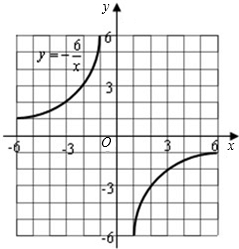似解．（结果保留两个有效数字）
19、利用图象解一元二次方程x2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x2和直线y=2x+1，两图象交点的横坐标就是该方程的解．