题目内容
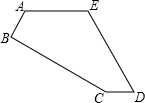 (2013•镇江)如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于
(2013•镇江)如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于13
| ||
| 4 |
13
| ||
| 4 |
分析:延长DC,AB交于点F,作AG∥DE交DF于点G,四边形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等边三角形,四边形AGDE是平行四边形,求得等腰梯形AFDE的面积和△BCF的面积,二者的差就是所求五边形的面积.
解答: 解:延长DC,AB交于点F,作AG∥DE交DF于点G.
解:延长DC,AB交于点F,作AG∥DE交DF于点G.
∵AE∥CD,∠A=∠E=120°,
∴四边形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等边三角形,四边形AGDE是平行四边形.
设BF=x,
∵在直角△BCF中,∠BCF=90°-∠F=30°
∴FC=2x,
∴FD=2x+1.
∵平行四边形AGDE中,DG=AE=2,
∴FG=2x-1,
∵△AFG是等边三角形中,AF=FG,
∴x+1=2x-1,
解得:x=2.
在直角△BCF中,BC=BF•tanF=2
,
则S△BCF=
BF•BC=
×2×2
=2
.
作AH⊥DF于点H.
则AH=AF•sinF=3×
=
,
则S梯形AFDE=
(AE+DF)•AH=
×(2+5)•
=
.
∴S五边形ABCDE=S梯形AFDE-S△BCF=
-2
=
.
故答案是:
.
 解:延长DC,AB交于点F,作AG∥DE交DF于点G.
解:延长DC,AB交于点F,作AG∥DE交DF于点G.∵AE∥CD,∠A=∠E=120°,
∴四边形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等边三角形,四边形AGDE是平行四边形.
设BF=x,
∵在直角△BCF中,∠BCF=90°-∠F=30°
∴FC=2x,
∴FD=2x+1.
∵平行四边形AGDE中,DG=AE=2,
∴FG=2x-1,
∵△AFG是等边三角形中,AF=FG,
∴x+1=2x-1,
解得:x=2.
在直角△BCF中,BC=BF•tanF=2
| 3 |
则S△BCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
作AH⊥DF于点H.
则AH=AF•sinF=3×
| ||
| 2 |
3
| ||
| 2 |
则S梯形AFDE=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
21
| ||
| 4 |
∴S五边形ABCDE=S梯形AFDE-S△BCF=
21
| ||
| 4 |
| 3 |
13
| ||
| 4 |
故答案是:
13
| ||
| 4 |
点评:本题考查了等腰梯形的判定与性质,直角三角形的性质,正确求得BF的长是关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
 (2013•镇江)如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=80°,则∠B=
(2013•镇江)如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=80°,则∠B= (2013•镇江)如图,A、B、C是反比例函数
(2013•镇江)如图,A、B、C是反比例函数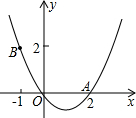 (2013•镇江)如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0).
(2013•镇江)如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0).