Question

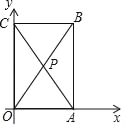
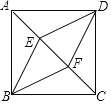
【题目】如图，E、F是正方形ABCD对角线AC上的两点，且，连接BE、DE、BF、DF．

求证：四边形BEDF是菱形：

求的值．

Answer 1

【答案】（1）证明见解析（2）3

【解析】

（1）连接BD交AC于点O，根据正方形的性质得到OA=OC，OB=OD，AC⊥BD，证明OE=OF，得到四边形BEDF是平行四边形，根据菱形的判定定理证明；

（2）根据正方形的性质得到OD=3OF，根据正切的定义计算，得到答案．

（1）连接BD交AC于点O．

∵四边形ABCD是正方形，∴OA=OC，OB=OD，且AC⊥BD．

∵AE=CF，∴OA﹣AE=OC﹣CF，即OE=OF．

又∵OB=OD，∴四边形BEDF是平行四边形．

又∵AC⊥BD，∴平行四边形BEDF是菱形；

（2）∵EF=2OF，EF=CF，∴CF=2OF，∴OC=3OF．

又∵OD=OC，∴OD=3OF．

在正方形ABCD中，AC⊥BD，∴∠DOF=90°．在Rt△DOF中，tan∠AFD3．