题目内容
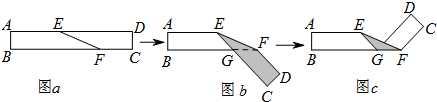
如图a是长方形纸带，∠DEF=22°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（ ）
| A、136 | B、92 |
| C、108 | D、114 |
考点：翻折变换（折叠问题）
专题：
分析：根据两直线平行，内错角相等可得∠EFB=∠DEF，再根据翻折的性质，图c中∠EFB处重叠了3层，然后根据∠CFE=180°-3∠EFB代入数据进行计算即可得解．
解答：解：∵∠DEF=22°，长方形ABCD的对边AD∥BC，
∴∠EFB=∠DEF=22°，
由折叠，∠EFB处重叠了3层，
∴∠CFE=180°-3∠EFB=180°-3×22°=114°．
故选D．
∴∠EFB=∠DEF=22°，
由折叠，∠EFB处重叠了3层，
∴∠CFE=180°-3∠EFB=180°-3×22°=114°．
故选D．
点评：本题考查了翻折变换，平行线的性质，观察图形判断出图c中∠EFB处重叠了3层是解题的关键．
练习册系列答案
相关题目
已知：x-y=5，（x+y）2=49，则x2+y2的值等于（ ）
| A、37 | B、27 | C、25 | D、44 |
如图，?ABCD中，AC．BD为对角线，BC=3，BC边上的高为2，则阴影部分的面积为（ ）| A、3 | B、6 | C、12 | D、24 |
估计
的大小应在（ ）
| 50 |
| A、5～6之间 |
| B、6～7之间 |
| C、7～8之间 |
| D、8～9之间 |
若（x-5y）2=（x+5y）2+M，则M的值为（ ）
| A、10xy | B、20xy |
| C、-10xy | D、-20xy |
如图是由相同的小正方体组成的几何体，它的俯视图为（ ）A、 |
B、 |
C、 |
D、 |