题目内容
已知：x-y=5，（x+y）2=49，则x2+y2的值等于（ ）
| A、37 | B、27 | C、25 | D、44 |
考点：完全平方公式
专题：计算题
分析：将x-y=5两边平方，利用完全平方公式展开，再将第二个等式左边利用完全平方公式展开，两式左右两边相加即可确定出所求式子的值．
解答：解：将x-y=5两边平方得：（x-y）2=x2+y2-2xy=25①，
再由（x+y）2=x2+y2+2xy=49②，
①+②得：2（x2+y2）=74，
则x2+y2=37．
故选A
再由（x+y）2=x2+y2+2xy=49②，
①+②得：2（x2+y2）=74，
则x2+y2=37．
故选A
点评：此题考查了完全平方公式，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
下列运算中，正确的是（ ）
| A、3a+5b=8ab |
| B、3y2-y2=3 |
| C、6a3+4a3=10a6 |
| D、5m2n-3nm2=2m2n |
下列多项式能分解因式的是（ ）
| A、x2+y2 | ||
| B、-x2-y2 | ||
| C、2xy-x2-y2 | ||
D、x2-xy+
|
下列运算正确的是（ ）
| A、a3+a3=a6 |
| B、a3•a3=a9 |
| C、a3÷a3=a |
| D、（a3）3=a9 |
a2+b2=5，ab=2，则（a+b）2=（ ）
| A、9 | B、10 | C、11 | D、12 |
如图a是长方形纸带，∠DEF=22°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（ ）
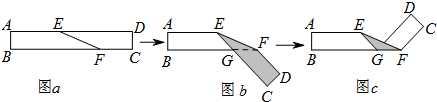
| A、136 | B、92 |
| C、108 | D、114 |