题目内容
1.对x,y定义一种新运算▲,规定:x▲y=ax+by(其中a,b均为非零常数),例如:1▲0=a,已知1▲1=3,-1▲1=-1.(1)求a,b的值;
(2)若关于m的不等式组$\left\{\begin{array}{l}{3m▲(1-2m)≤4}\\{2m▲m>p}\end{array}\right.$恰有3个整数解,求实数p的取值范围.
分析 (1)利用题中的新定义化简已知两式,得到关于a与b的方程组,求出方程组的解即可得到a与b的值;
(2)把a与b的值代入确定出x▲y=2x+y,表示不等式组变形后表示出解集,根据解集恰有3个整数解确定出p的范围即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a+b=3}\\{-a+b=-1}\end{array}\right.$,
解得:a=2,b=1;
(2)不等式变形得:$\left\{\begin{array}{l}{6m+1-2m≤4①}\\{4m+m>p②}\end{array}\right.$,
由①得:m≤$\frac{3}{4}$,
由②得:m>$\frac{p}{5}$,
不等式组的解集为$\frac{p}{5}$<m≤$\frac{3}{4}$,
由不等式组恰有3个整数解,即0,-1,-2,
得到-3≤$\frac{p}{5}$<-2,
解得:-15≤p<-10.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
16.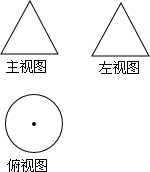 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | $\sqrt{3}$π |
6.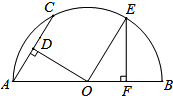 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
10.计算a3•(-$\frac{1}{a}$)2的结果是( )
| A. | a | B. | a5 | C. | a6 | D. | a4 |
 已知正方形的边长为a,内有一个内接圆,求阴影面积.
已知正方形的边长为a,内有一个内接圆,求阴影面积.