Question

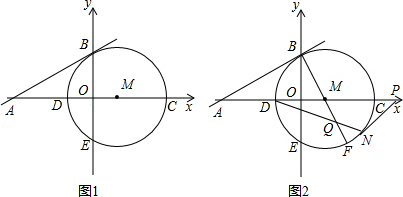
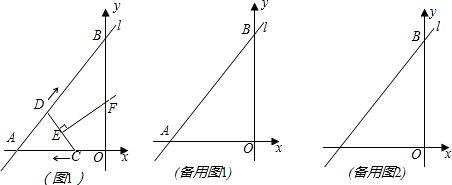
29、如图1，已知直线m∥n，点A、B在直线n上，点C、P在直线m上；
（1）写出图1中面积相等的各对三角形：

△CAB与△PAB、△BCP与△APC、△ACO与△BOP

；
（2）如图①，A、B、C为三个顶点，点P在直线m上移动到任一位置时，总有

△PAB

与△ABC的面积相等；
（3）如图②，一个五边形ABCDE，你能否过点E作一条直线交BC（或延长线）于点M，使四边形ABME的面积等于五边形ABCDE的面积．

Answer 1

分析：（1）找出图①中同底等高的三角形，这些三角形的面积相等；
（2）因为两平行线间的距离是相等的，所以点C、P到直线n间的距离相等，也就是说△ABC与△PAB的公共边AB上的高相等，所以总有△PAB与△ABC的面积相等；
（3）只要作一个三角形CEM与三角形CED的面积相等即可．

解答：解：（1）∵m∥n，
∴点C、P到直线n间的距离与点A、B到直线m间的距离相等；
又∵同底等高的三角形的面积相等，
∴图①中符合条件的三角形有：△CAB与△PAB、△BCP与△APC，△ACO与△BOP；

（2）∵m∥n，
∴点C、P到直线n间的距离是相等的，
∴△ABC与△PAB的公共边AB上的高相等，
∴总有△PAB与△ABC的面积相等；

（3）
连接EC，过点D作直线DM∥EC交BC延长线于点M，连接EM，线段EM所在的直线即为所求的直线．

点评：本题主要考查了三角形的面积及平行线的性质，利用平行线间的距离相等得到同底等高的三角形是解题的关键．