Question

如图1，已知直线：y=

3

3

x+

3

与直角坐标系xOy的x轴交于点A，与y轴交于点B，点M为x轴正半轴上一点，以点M为圆心的⊙M与直线AB相切于B点，交x轴于C、D两点，与y轴交于另一点E．
（1）求圆心M的坐标；
（2）如图2，连接BM延长交⊙M于F，点N为

CF

上任一点，连DN交BF于Q，连FN并延长交x轴于点P．则CP与MQ有何数量关系？证明你的结论；
（3）如图3，连接BM延长交⊙M于F，点N为

CF

上一动点，NH⊥x轴于H，NG⊥BF于G，连接GH，当N点运动时，下列两个结论：①NG+NH为定值；②GH的长度不变；其中只有一个是正确的，请你选择正确的结论加以证明，并求出其值？

Answer 1

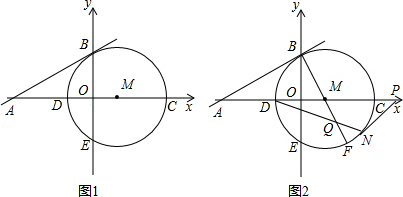
分析：（1）根据一次函数解析式求出A，B两点的坐标．进而得出AO，BO的长，再利用射影定理求出MO的长即可得出答案；
（2）利用圆周角定理以及等边三角形的性质得出△BDQ≌△MFP，进而得到PM=BQ，从而得出CP与MQ的数量关系；
（3）根据垂径定理以及锐角三角函数首先得出WQ=2

3

，进而得出GH是△WNQ的中位线，HG=

1

2

WQ=

3

，即可得出答案．

解答：解：（1）连接BM，
∵y=

3

3

x+

3

与直角坐标系xOy的x轴交于点A，与y轴交于点B，
∴A点横坐标为x：0=

3

3

x+

3

，纵坐标为0，
∴x=-3，A（-3，0），
B点坐标为：（0，

3

），
∴BO=

3

，AO=3，
∵以点M为圆心的⊙M与直线AB相切于B点，
∴AB⊥BM，
∵BO⊥AM．
∴BO²=AO×MO，
3=3MO，
∴MO=1，
∴圆心M的坐标为（1，0）；

（2）MQ=PC．
证明：∵BO=

3

，MO=1，
∴tan∠BMO=

3

，
∴∠BMO=60°，
∵BM=DM，
∴△BDM是等边三角形，
∴BD=BM=DM，∠DBQ=60°，
∴∠FMP=∠BMD=60°，
∴∠DBQ=∠FMP=60°，
∵∠BDN=∠BFN，
∴△BDQ≌△MFP，
∴PM=BQ，
∵BM=CM，
∴BQ-BM=PM-MC，
即：MQ=PC；

（3）GH的长度不变；
证明：延长NH到⊙一点Q，延长NG到圆上一点W，作MT⊥WQ，连接WQ，MQ，MW，MN，
∵NH⊥x轴于H，NG⊥BF于G，
∴QC=CN，GN=WQ，

QC

=

CN

，

WF

=

FN

，（垂径定理的推论）
∴∠QMC=∠CMN，∠NMF=∠FMW，
∵由（2）得出∠DMB=∠FMC=60°，
∴∠WMQ=120°，WM=MQ，
∴QT=WT，∠TMQ=60°，
∵DM=MQ=2，
∴sin60°=

QT

2

，
∴QT=

3

，
∴WQ=2

3

，
∴点N为

CF

上一动点，到什么位置△WMQ形状不变，
∴QW=2

3

长度不变，
∵H为QN的中点，G为WN的中点，
∴GH是△WNQ的中位线，
∴HG=

1

2

WQ=

3

，
∴GH的长度不变．

点评：此题主要考查了圆周角定理以及全等三角形的判定和锐角三角函数等知识，所以同学们学习时一定要会把所学的知识灵活的运用起来，延长NC到⊙一点Q，延长NG到圆上一点W，得出这两条辅助线是解决问题的关键．