题目内容
6.将函数y=3x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|3x+b|(b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<2,则b的取值范围为-5≤b≤-1.分析 先解不等式3x+b<1时,得x<$\frac{1-b}{3}$;再求出函数y=3x+b沿x轴翻折后的解析式为y=-3x-b,解不等式-3x-b<1,得x>-$\frac{1+b}{3}$;根据x满足0<x<2,得出-$\frac{1+b}{3}$=0,$\frac{1-b}{3}$=2,进而求出b的取值范围.
解答 解:∵y=3x+b,
∴当y<1时,3x+b<1,解得x<$\frac{1-b}{3}$;
∵函数y=3x+b沿x轴翻折后的解析式为-y=3x+b,即y=-3x-b,
∴当y<1时,-3x-b<1,解得x>-$\frac{1+b}{3}$;
∴-$\frac{1+b}{3}$<x<$\frac{1-b}{3}$,
∵x满足0<x<2,
∴-$\frac{1+b}{3}$=0,$\frac{1-b}{3}$=2,
∴b=-1,b=-5,
∴b的取值范围为-5≤b≤-1.
故答案为-5≤b≤-1.
点评 本题考查了一次函数图象与几何变换,求出函数y=3x+b沿x轴翻折后的解析式是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
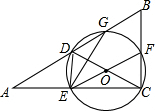 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点. 画出如图几何体的从正面、从左面、从上面看到的形状图.
画出如图几何体的从正面、从左面、从上面看到的形状图.