题目内容
已知一次函数y=mx+n与反比例函数y= 的图象相交于点( 1,2 ),求该直线与双曲线的另一个交点坐标________.
的图象相交于点( 1,2 ),求该直线与双曲线的另一个交点坐标________.
(-2,-1)
分析:由一次函数y=mx+n与反比例函数y= 的图象相交于点( 1,2).联立列方程组,求得m、n的值,再求另一个交点坐标.
的图象相交于点( 1,2).联立列方程组,求得m、n的值,再求另一个交点坐标.
解答:∵直线y=mx+n与双曲线y= 相交于( 1,2),
相交于( 1,2),
∴ .
.
解得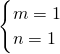 .
.
∴直线为y=x+1.
双曲线为y= .
.
解方程组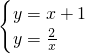 ,
,
解得 ,
, .
.
∴另一个交点为(-2,-1).
故答案为:(-2,-1).
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.
分析:由一次函数y=mx+n与反比例函数y=
 的图象相交于点( 1,2).联立列方程组,求得m、n的值,再求另一个交点坐标.
的图象相交于点( 1,2).联立列方程组,求得m、n的值,再求另一个交点坐标.解答:∵直线y=mx+n与双曲线y=
 相交于( 1,2),
相交于( 1,2),∴
 .
.解得
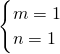 .
.∴直线为y=x+1.
双曲线为y=
 .
.解方程组
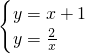 ,
,解得
 ,
, .
.∴另一个交点为(-2,-1).
故答案为:(-2,-1).
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 已知一次函数y=mx+n(m≠0)与反比例函数
已知一次函数y=mx+n(m≠0)与反比例函数