题目内容
20.若|x+4|与|2y-4|互为相反数,则x+y=-2.分析 利用绝对值的性质以及互为相反数的性质得出x+4=0,2y-4=0,进而求出答案.
解答 解:∵|x+4|和|2y-4|互为相反数,
∴|x+4|+|2y-4|=0,
∴x+4=0,2y-4=0,
解得:x=-4,y=2,
∴x+y=-4+2=-2.
故答案为:-2.
点评 此题主要考查了绝对值以及相反数的定义,求出x,y的值是解题关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
10.下列计算中,正确的是( )
| A. | a•a=2a | B. | (2a)3=6a3 | C. | a+2a=3a2 | D. | a6÷a4=a2 |
9.正n边形的边数每增加一条,其内角就增加( )
| A. | $\frac{180°}{n}$ | B. | $\frac{180°}{n+1}$ | C. | $\frac{180°}{n-1}$ | D. | $\frac{360°}{n(n+1)}$ |
10.若-[-(a-b)]是负数,则下列各式成立的是( )
| A. | a-b>0 | B. | a-b<0 | C. | a-b≥0 | D. | a-b≤0 |
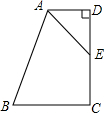 如图.已知AD∥BC,DC⊥AD,∠BAD的平分线交CD于点E,且点E是CD的中点.问:
如图.已知AD∥BC,DC⊥AD,∠BAD的平分线交CD于点E,且点E是CD的中点.问: