Question

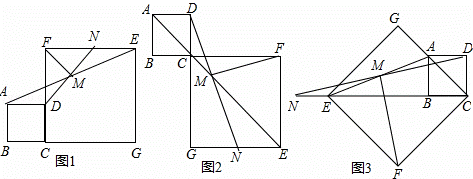
如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）

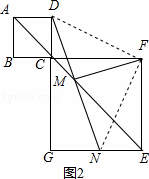
（1）如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；

（2）如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．

　

Answer 1

 解：（1）如图2，DM=FM，DM⊥FM，

证明：连接DF，NF，

∵四边形ABCD和CGEF是正方形，

∴AD∥BC，BC∥GE，

∴AD∥GE，

∴∠DAM=∠NEM，

∵M是AE的中点，

∴AM=EM，

在△MAD与△MEN中，

，

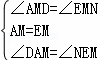∴△MAD≌△MEN，

∴DM=MN，AD=EN，

∵AD=CD，

∴CD=NE，

∵CF=EF，∠DCF=∠DCB=90°，

在△DCF与△NEF中，

，

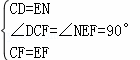∴△MAD≌△MEN，

∴DF=NF，∠CFD=∠EFN，

∵∠EFN+∠NFC=90°，

∴∠DFC+∠CFN=90°，

∴∠DFN=90°，

∴DM⊥FM，DM=FM

（2）猜想：DM⊥FM，DM=FM，

证明如下：如图3，连接DF，NF，

连接DF，NF，

∵四边形ABCD是正方形，

∴AD∥BC，

∵点E、B、C在同一条直线上，

∴AD∥CN，

∴∠ADN=∠MNE，

在△MAD与△MEN中，

，

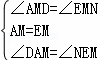∴△MAD≌△MEN，

∴DM=MN，AD=EN，

∵AD=CD，

∴CD=NE，

∵CF=EF，

∵∠DCF=90°+45°=135°，∠NEF=180°﹣45°=135°，

∴∠DCF=∠NEF，

在△DCF与△NEF中，

，

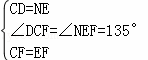∴△MAD≌△MEN，

∴DF=NF，∠CFD=∠EFN，

∵∠CFD+∠EFD=90°，

∴∠NFE+∠EFD=90°，

∴∠DFN=90°，

∴DM⊥FM，DM=FM．