题目内容
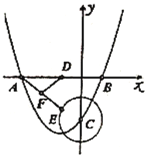
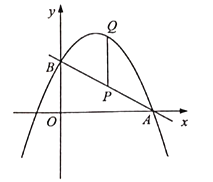
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() ),与
),与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
(1)当![]() 时,
时,
①求抛物线的关系式;
②设点![]() 的横坐标为
的横坐标为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的长,并求当
的长,并求当![]() 为何值时,
为何值时,![]() ?
?
(2)若![]() 长的最大值为16,试讨论关于
长的最大值为16,试讨论关于![]() 的一元二次方程
的一元二次方程![]() 的解的个数与
的解的个数与![]() 的取值范围的关系.
的取值范围的关系.
【答案】(1)①![]() ;②
;②![]() ;当x=1或x=4时,
;当x=1或x=4时,![]() ;(2)当
;(2)当![]() 时,一元二次方程
时,一元二次方程![]() 有一个解;当
有一个解;当![]() >16时,一元二次方程
>16时,一元二次方程![]() 无解;当
无解;当![]() <16时,一元二次方程
<16时,一元二次方程![]() 有两个解.
有两个解.
【解析】
(1)①首先根据题意得出点A、B的坐标,然后代入抛物线解析式即可得出其表达式;
②首先由点A的坐标得出直线解析式,然后得出点P、Q坐标,根据平行构建方程,即可得解;
(2)首先得出![]() ,然后由PQ的最大值得出
,然后由PQ的最大值得出![]() 最大值,再利用二次函数图象的性质分类讨论一元二次方程的解即可.
最大值,再利用二次函数图象的性质分类讨论一元二次方程的解即可.
(1)①∵m=5,
∴点A的坐标为(5,0).
将x=0代入![]() ,得y=2.
,得y=2.
∴点B的坐标为(0,2).
将A(5,0),B(0,2)
代入![]() ,得
,得
![]() 解得
解得 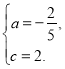
∴抛物线的表达式为![]() .
.
②将A(5,0)代入![]() ,解得:
,解得:![]() .
.
∴一次函数的表达为![]() .
.
∴点P的坐标为![]() ,
,
又∵PQ∥y轴,
∴点Q的坐标为![]()
∴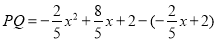
![]()
∵![]() ,
,
∴![]()
解得:![]() ,
,![]()
∴当x=1或x=4时,![]() ;
;
(2)由题意知:![]()
设![]() ,
,
∴![]() 为
为![]() 的二次函数,又
的二次函数,又![]() <
<![]() ,
,
∵![]() 长的最大值为16,
长的最大值为16,
∴![]() 最大值为16.
最大值为16.
∴由二次函数的图象性质可知
当![]() 时,一元二次方程
时,一元二次方程![]() 有一个解;
有一个解;
当![]() >16时,一元二次方程
>16时,一元二次方程![]() 无解;
无解;
当![]() <16时,一元二次方程
<16时,一元二次方程![]() 有两个解..
有两个解..

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目