题目内容
 如图,AC、BD相交于点G,E、F分别在AB、AG上,连接EF、FD、DC.若∠A=∠C,
如图,AC、BD相交于点G,E、F分别在AB、AG上,连接EF、FD、DC.若∠A=∠C, ,则图中共有相似三角形
,则图中共有相似三角形
- A.1对
- B.2对
- C.3对
- D.4对
C
分析:两组对应角相等,那么这两个三角形相似,如果两组对应边成比例,夹角相等那么这两个三角形相似,根据这些判定定理可找出相似三角形的对数.
解答:∵∠A=∠C,
∴AB∥CD,
∴∠B=∠CDB,
∴△ABG∽△CDG.
∵ =
=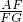 ,∠A=∠A,
,∠A=∠A,
∴△AEF∽△ABG.
∵∠A=∠C,∠CDG=∠AEF,
∴△AEF∽△CDG.
所以有3对三角形相似.
故选C.
点评:本题考查相似三角形的判定定理,两组对应角相等,那么这两个三角形相似,如果两组对应边成比例,夹角相等那么这两个三角形相似.
分析:两组对应角相等,那么这两个三角形相似,如果两组对应边成比例,夹角相等那么这两个三角形相似,根据这些判定定理可找出相似三角形的对数.
解答:∵∠A=∠C,
∴AB∥CD,
∴∠B=∠CDB,
∴△ABG∽△CDG.
∵
 =
=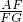 ,∠A=∠A,
,∠A=∠A,∴△AEF∽△ABG.
∵∠A=∠C,∠CDG=∠AEF,
∴△AEF∽△CDG.
所以有3对三角形相似.
故选C.
点评:本题考查相似三角形的判定定理,两组对应角相等,那么这两个三角形相似,如果两组对应边成比例,夹角相等那么这两个三角形相似.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 8、如图,AC,BD相交于点O,AC=BD,AB=CD,写出图中两对相等的角
8、如图,AC,BD相交于点O,AC=BD,AB=CD,写出图中两对相等的角 14、如图,AC和BD相交于点O,OA=OC,要使△AOB≌△COD还需添加一个条件是
14、如图,AC和BD相交于点O,OA=OC,要使△AOB≌△COD还需添加一个条件是 22、如图,AC与BD相交于点P,若△ABC≌△DCB,则△ABP≌△DCP,理由是:
22、如图,AC与BD相交于点P,若△ABC≌△DCB,则△ABP≌△DCP,理由是: 12、如图,AC与BD相交于点O,已知OA=OC,OB=OD,则△AOB≌△COD的理由是
12、如图,AC与BD相交于点O,已知OA=OC,OB=OD,则△AOB≌△COD的理由是 如图,AC,BD相交于点O,且AB=DC,AC=DB.求证:∠ABO=∠DCO.
如图,AC,BD相交于点O,且AB=DC,AC=DB.求证:∠ABO=∠DCO.