题目内容
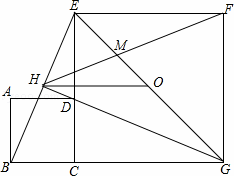
如图,正方形ABCD的边CD与正方形CGEF的边CE重合,O是EG的中点,∠EGC的评分项GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
①GH⊥BE;②HO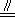
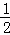 BG;③点H不在正方形CGFE的外接圆上;④△GBE∽△GMF.
BG;③点H不在正方形CGFE的外接圆上;④△GBE∽△GMF.
其中正确的结论有( )
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
C
解:(1)如图,∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,

∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①正确,
(2)∵GH是∠EGC的平分线,
∴∠BGH=∠EGH,
在△BGH和△EGH中

∴△BGH≌△EGH(ASA),
∴BH=EH,
∵O是EG的中点,
∴ =
= =
= ,
,
∴HO= BG,
BG,
故②正确.
(3)由(1)得△EHG是直角三角形,
∵O为FG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
故③错误,
(4)如图2,连接CF,

由(3)可得点H在正方形CGFE的外接圆上,
∴∠HFC=∠CGH,
∵∠HFC+∠FMG=90°,∠CGH+∠GBE=90°,
∴∠FMG=∠GBE,
又∵∠EGB=∠FGM=45°,
∴△GBE∽△GMF.

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案对参加某次野外训练的中学生的年龄(单位:岁)进行统计,结果如表:
| 年龄 | 13 | 14 | 15 | 16 | 17 | 18 |
| 人数 | 4 | 5 | 6 | 6 | 7 | 2 |
则这些学生年龄的众数和中位数分别是( )
|
| A. | 17,15.5 | B. | 17,16 | C. | 15,15.5 | D. | 16,16 |
因式分解a2b﹣b的正确结果是( )
|
| A. | b(a+1)(a﹣1) | B. | a(b+1)(b﹣1) | C. | b(a2﹣1) | D. | b(a﹣1)2 |
为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
|
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) |
| 甲型挖掘机 | 100 | 60 |
| 乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
已知一组数据:1,2,6,3,3,下列说法正确的是( )
|
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是4 | D. | 方差是5 |

