题目内容
【题目】某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.
(1)若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.
(3)若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?
【答案】
(1)解:设小王够买A品牌文具x套,够买B品牌文具y套,
根据题意,得: ![]() ,
,
解得: ![]() ,
,
答:小王够买A品牌文具600套,够买B品牌文具400套
(2)解:y=500+0.8[20x+25(1000﹣x)]
=500+0.8(25000﹣5x)
=500+20000﹣4x
=﹣4x+20500,
∴y与x之间的函数关系式是:y=﹣4x+20500
(3)解:根据题意,得:﹣4x+20500=20000,解得:x=125,
∴小王够买A品牌文具套装为125套、够买B品牌文具套装为875套,
设A品牌文具套装的售价为z元,则B品牌文具套装的售价为(z+5)元,
由题意得:125z+875(z+5)≥20000+8×1000,
解得:z≥23.625,
答:A品牌的文具套装每套定价不低于24元时才不亏本
【解析】(1)设小王需购买A、B两种品牌文具套装分别为x套、y套,则 ![]() ,据此求出小王购买A、B两种品牌文具套装分别为多少套即可.(2)根据题意,可得y=500+0.8×[20x+25(1000﹣x)],据此求出y与x之间的函数关系式即可.(3)首先求出小王购买A、B两种品牌文具套装分别为多少套,然后设A品牌文具套装的售价为z元,则B品牌文具套装的售价为z+5元,所以125z+875(z+5)≥20000+8×1000,据此求出A品牌的文具套装每套定价不低于多少元时才不亏本即可.
,据此求出小王购买A、B两种品牌文具套装分别为多少套即可.(2)根据题意,可得y=500+0.8×[20x+25(1000﹣x)],据此求出y与x之间的函数关系式即可.(3)首先求出小王购买A、B两种品牌文具套装分别为多少套,然后设A品牌文具套装的售价为z元,则B品牌文具套装的售价为z+5元,所以125z+875(z+5)≥20000+8×1000,据此求出A品牌的文具套装每套定价不低于多少元时才不亏本即可.

 计算高手系列答案
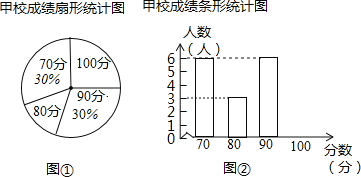
计算高手系列答案【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表 | |
分数 | 人数 |
70 | 7 |
80 | ______ |
90 | 1 |
100 | 8 |
![]() 乙学校的参赛人数是______人
乙学校的参赛人数是______人![]()
![]() 在图
在图![]() 中,“80分”所在扇形的圆心角度数为______;
中,“80分”所在扇形的圆心角度数为______;
![]() 请你将图
请你将图![]() 补充完整;
补充完整;
![]() 求乙校成绩的平均分.
求乙校成绩的平均分.