题目内容
等腰三角形腰长为2cm,面积为1cm,则这个等腰三角形的底角的余弦值为
.
| ||||
| 4 |
| ||||
| 4 |
分析:先画图,再过A作AD⊥BC于D,由于AB=AC,AD⊥BC,利用等腰三角形三线合一定理可知BD=CD,再设BD=CD=x,AD=y,
根据面积是1可得xy=1①,再根据勾股定理可得x2+y2=4②,①②联合可求y=
,进而可求底角的余弦值.
根据面积是1可得xy=1①,再根据勾股定理可得x2+y2=4②,①②联合可求y=
| ||||
| 2 |
解答: 解:如右图,△ABC是等腰三角形,且AB=AC,
解:如右图,△ABC是等腰三角形,且AB=AC,
过A作AD⊥BC于D,
∵AB=AC,AD⊥BC,
∴BD=CD,
设BD=CD=x,AD=y,
∵S△ABC=1,
∴xy=1①,
在Rt△ABD中,
x2+y2=4②,
①×2+②可得x+y=
(负数不合题意,舍去),
②-①×2可得x-y=±
,
∴y=
,
∴cos∠B=
=
.
 解:如右图,△ABC是等腰三角形,且AB=AC,
解:如右图,△ABC是等腰三角形,且AB=AC,过A作AD⊥BC于D,
∵AB=AC,AD⊥BC,
∴BD=CD,
设BD=CD=x,AD=y,
∵S△ABC=1,
∴xy=1①,
在Rt△ABD中,
x2+y2=4②,
①×2+②可得x+y=
| 6 |
②-①×2可得x-y=±
| 2 |
∴y=
| ||||
| 2 |
∴cos∠B=
| AD |
| AB |
| ||||
| 4 |
点评:本题考查了解直角三角形,解题的关键是注意作底边上的高,并且利用勾股定理,要考虑两种情况.

练习册系列答案
相关题目





 ,周长为
,周长为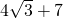 ,那么这个等腰三角形的腰长为
,那么这个等腰三角形的腰长为
 ,则腰长为( )
,则腰长为( )