题目内容
等腰三角形一边长为2 ,周长为
,周长为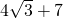 ,那么这个等腰三角形的腰长为
,那么这个等腰三角形的腰长为
- A.3.5

- B.2

- C.3.52
- D.不能确定
A
分析:已知条件中,本题没有明确说明已知的边长是否是腰长,所以有两种情况讨论,再根据三角形的周长公式进行解答,然后进行判定能否组成三角形,即可求出答案.
解答:①底边长为3,则腰长为:(4 +7-2
+7-2 )÷2=3.5+
)÷2=3.5+ ,所以另两边的长为3.5
,所以另两边的长为3.5 ,3.5
,3.5 ,能构成三角形;
,能构成三角形;
②腰长为2 ,则底边长为:4
,则底边长为:4 +7-4
+7-4 =7,底边长为7,另一个腰长2
=7,底边长为7,另一个腰长2 ,2
,2 +2
+2 <7,不能构成三角形.
<7,不能构成三角形.
因此另两边长为3.5+ ,
,
故选A.
点评:本题考查了二次根式的应用;解题的关键是根据等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要.
分析:已知条件中,本题没有明确说明已知的边长是否是腰长,所以有两种情况讨论,再根据三角形的周长公式进行解答,然后进行判定能否组成三角形,即可求出答案.
解答:①底边长为3,则腰长为:(4
 +7-2
+7-2 )÷2=3.5+
)÷2=3.5+ ,所以另两边的长为3.5
,所以另两边的长为3.5 ,3.5
,3.5 ,能构成三角形;
,能构成三角形;②腰长为2
 ,则底边长为:4
,则底边长为:4 +7-4
+7-4 =7,底边长为7,另一个腰长2
=7,底边长为7,另一个腰长2 ,2
,2 +2
+2 <7,不能构成三角形.
<7,不能构成三角形.因此另两边长为3.5+
 ,
,故选A.
点评:本题考查了二次根式的应用;解题的关键是根据等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要.

练习册系列答案
相关题目