Question

【题目】在平面直角坐标系中，O为原点，B（0，6），A（8，0），以点B为旋转中心把△ABO逆时针旋转，得△A′BO′，点O，A旋转后的对应点为O′，A′，记旋转角为β．

（1）如图1，若β＝90°，求AA′的长；

（2）如图2，若β＝120°，求点O′的坐标．

Answer 1

【答案】(1)10;(2)(3,9)

【解析】试题分析：（1）根据旋转角求出 根据点的坐标求出 利用勾股定理列式求出 ，再根据旋转的性质可得 然后利用勾股定理列式计算即可得解；
（2）过点作轴于 根据旋转的性质求出 再求出 然后解直角三角形求出 再求出 然后写出点的坐标即可．

试题解析：

∵A(8,0),B(0,6)，

∴OA=8，OB=6，

根据勾股定理得,

由旋转的性质得,A′B=AB=10，

在中,根据勾股定理得,

(2)如图,过点O′作O′C⊥y轴于C，

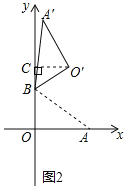
由旋转的性质得,O′B=OB=6，

∴点O′的坐标为