Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ÷ō«ž“Ľ÷–Ņ™—ß≥ű‘ŕ÷ōįŔ…Ő≥°Ķŕ“ĽīőĻļĹÝA°ĘBŃĹ÷÷∆∑Ň∆Ķń◊„«Ú£¨Ļļ¬ÚA∆∑Ň∆◊„«ÚĽ®∑—Ńň3200‘™£¨Ļļ¬ÚB∆∑Ň∆◊„«ÚĽ®∑—Ńň2400‘™£¨«“Ļļ¬ÚA∆∑Ň∆◊„«Ú żŃŅ «Ļļ¬ÚB∆∑Ň∆◊„«Ú żŃŅĶń2Ī∂£¨“—÷™Ļļ¬Ú“ĽłŲB∆∑Ň∆◊„«ÚĪ»Ļļ¬Ú“ĽłŲA∆∑Ň∆Ķń◊„«Ú∂ŗĽ®20‘™£ģ
£®1£©«ůĻļ¬Ú“ĽłŲA∆∑Ň∆°Ę“ĽłŲB∆∑Ň∆Ķń◊„«Úłų–Ť∂ŗ…Ŕ‘™£Ľ
£®2£©÷ō«ž“Ľ÷–ő™ĺŔįž◊„«ÚŃ™“Í»Ł£¨ĺŲ∂®Ķŕ∂ĢīőĻļĹÝA°ĘBŃĹ÷÷∆∑Ň∆◊„«Ú£ģ«°∑Í÷ōįŔ…Ő≥°∂‘ŃĹ÷÷∆∑Ň∆◊„«ÚĶń ŘľŘĹÝ––Ķų’Ż£¨A∆∑Ň∆◊„«Ú ŘľŘĪ»Ķŕ“ĽīőĻļ¬Ú ĪŐŠłŖŃňa‘™£®a£ĺ0£©£¨B∆∑Ň∆◊„«ÚįīĶŕ“ĽīőĻļ¬Ú Ī ŘľŘĶń9’Ř≥Ų Ř£ģ»ÁĻŻĶŕ∂ĢīőĻļ¬ÚA∆∑Ň∆◊„«ÚĶńłŲ żĪ»Ķŕ“Ľīő…Ŕ2ałŲ£¨Ķŕ∂ĢīőĻļ¬ÚB∆∑Ň∆◊„«ÚĶńłŲ żĪ»Ķŕ“Ľīő∂ŗ![]() łŲ£¨‘ÚĶŕ∂ĢīőĻļ¬ÚA°ĘBŃĹ÷÷∆∑Ň∆◊„«ÚĶń◊‹∑—”√Ī»Ķŕ“Ľīő…Ŕ320‘™£¨«ůaĶń÷Ķ£ģ
łŲ£¨‘ÚĶŕ∂ĢīőĻļ¬ÚA°ĘBŃĹ÷÷∆∑Ň∆◊„«ÚĶń◊‹∑—”√Ī»Ķŕ“Ľīő…Ŕ320‘™£¨«ůaĶń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©Ļļ¬Ú“ĽłŲA∆∑Ň∆Ķń◊„«Ú–Ť40‘™£¨“ĽłŲB∆∑Ň∆Ķń◊„«Ú–Ť60‘™£Ľ£®2£©aĶń÷Ķ «16
°ĺĹ‚őŲ°Ņ
£®1£©…ŤĻļ¬ÚA÷÷∆∑Ň∆◊„«ÚĶńĶ•ľŘő™x‘™/łŲ£¨Ļļ¬ÚB÷÷∆∑Ň∆◊„«ÚĶńĶ•ľŘő™£®x+20£©‘™/łŲ£¨łýĺ›Ļļ¬ÚA∆∑Ň∆◊„«ÚĽ®∑—Ńň3200‘™£¨Ļļ¬ÚB∆∑Ň∆◊„«ÚĽ®∑—Ńň2400‘™£¨«“Ļļ¬ÚA∆∑Ň∆◊„«Ú żŃŅ «Ļļ¬ÚB∆∑Ň∆◊„«Ú żŃŅĶń2Ī∂£¨ľīŅ…Ķ√≥ŲĻō”ŕxĶń∑Ĺ≥Ő£¨Ĺ‚÷ģľīŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
£®2£©łýĺ›Ķŕ∂ĢīőĻļ¬ÚA∆∑Ň∆◊„«ÚĶńłŲ żĪ»Ķŕ“Ľīő…Ŕ2ałŲ£¨Ķŕ∂ĢīőĻļ¬ÚB∆∑Ň∆◊„«ÚĶńłŲ żĪ»Ķŕ“Ľīő∂ŗ![]() łŲ£¨‘ÚĶŕ∂ĢīőĻļ¬ÚA°ĘBŃĹ÷÷∆∑Ň∆◊„«ÚĶń◊‹∑—”√Ī»Ķŕ“Ľīő…Ŕ320‘™£¨Ń–≥Ų∑Ĺ≥ŐĹ‚ĺŲő Ő‚£ģ
łŲ£¨‘ÚĶŕ∂ĢīőĻļ¬ÚA°ĘBŃĹ÷÷∆∑Ň∆◊„«ÚĶń◊‹∑—”√Ī»Ķŕ“Ľīő…Ŕ320‘™£¨Ń–≥Ų∑Ĺ≥ŐĹ‚ĺŲő Ő‚£ģ
Ĺ‚£ļ£®1£©…ŤĻļ¬Ú“ĽłŲA∆∑Ň∆Ķń◊„«Ú–Ťx‘™£¨‘Ú“ĽłŲB∆∑Ň∆Ķń◊„«Ú–Ť£®x+20£©‘™£¨”…Ő‚“‚Ķ√£¨
![]() £Ĺ
£Ĺ![]() °Ń2£¨
°Ń2£¨
Ĺ‚Ķ√£ļx£Ĺ40£¨
ĺ≠ľž—ťx£Ĺ40 «‘≠∑Ĺ≥ŐĶńĹ‚£¨
x+20£Ĺ60£¨
īū£ļĻļ¬Ú“ĽłŲA∆∑Ň∆Ķń◊„«Ú–Ť40‘™£¨“ĽłŲB∆∑Ň∆Ķń◊„«Ú–Ť60‘™£ģ
£®2£©”…£®1£©Ņ…÷™£¨Ķŕ“ĽīőĻļ¬ÚA∆∑Ň∆Ķń◊„«ÚłŲ żő™£ļ3200°¬40=80£®łŲ£©£¨‘ÚĻļ¬ÚB∆∑Ň∆Ķń◊„«ÚłŲ żő™40łŲ£¨
“ņŐ‚“‚Ķ√£ļ£®40+a£©£®80©Ā2a£©+60°Ń0.9£®40+![]() £©£Ĺ2400+3200©Ā320£¨
£©£Ĺ2400+3200©Ā320£¨
ĽĮľÚĶ√2a2©Ā27a©Ā80£Ĺ0£¨
°ŗa1£Ĺ©Ā2.5£®…Š»•£©£¨a2£Ĺ16£ģ
īū£ļaĶń÷Ķ «16£ģ

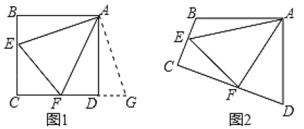
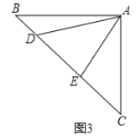
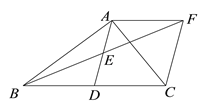
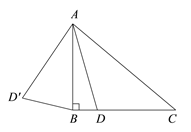
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°ųABC÷–£¨ ![]() £¨
£¨ ![]() °„£¨Ķ„D «ŌŖ∂őBC…ŌĶń∂ĮĶ„£¨ĹęŌŖ∂őAD»∆Ķ„Aň≥ Ī’Ž–ż◊™50°„÷Ń
°„£¨Ķ„D «ŌŖ∂őBC…ŌĶń∂ĮĶ„£¨ĹęŌŖ∂őAD»∆Ķ„Aň≥ Ī’Ž–ż◊™50°„÷Ń![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £ģ“—÷™AB
£ģ“—÷™AB![]() 2cm£¨…ŤBDő™x cm£¨B
2cm£¨…ŤBDő™x cm£¨B![]() ő™y cm£ģ
ő™y cm£ģ
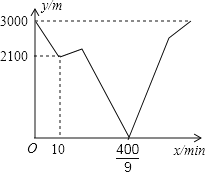
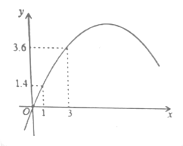
–°√ųłýĺ›—ßŌįļĮ żĶńĺ≠—ť£¨∂‘ļĮ żyňś◊‘ĪšŃŅxĶńĪšĽĮ∂ÝĪšĽĮĶńĻś¬…ĹÝ––ŃňŐĹĺŅ£¨Ō¬√ś «–°√ųĶńŐĹĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ’Ż£ģ£®ňĶ√ų£ļĹ‚īū÷–ňýŐÓ ż÷ĶĺýĪ£ŃŰ“ĽőĽ–° ż£©
£®1£©Õ®Ļż»°Ķ„°ĘĽ≠Õľ°Ę≤‚ŃŅ£¨Ķ√ĶĹŃň![]() ”Ž
”Ž![]() Ķńľł◊ť÷Ķ£¨»ÁŌ¬ĪŪ£ļ
Ķńľł◊ť÷Ķ£¨»ÁŌ¬ĪŪ£ļ
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
£®2£©Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨√Ť≥Ų“‘≤Ļ»ęļůĶńĪŪ÷–łų∂‘∂‘”¶÷Ķő™◊ÝĪÍĶńĶ„£¨Ľ≠≥Ųł√ļĮ żĶńÕľŌů£ģ

£®3£©ĹŠļŌĽ≠≥ŲĶńļĮ żÕľŌů£¨Ĺ‚ĺŲő Ő‚£ļ
ŌŖ∂ő![]() Ķń≥§∂»Ķń◊Ó–°÷Ķ‘ľő™__________
Ķń≥§∂»Ķń◊Ó–°÷Ķ‘ľő™__________ ![]() £Ľ
£Ľ
»Ű![]()
![]() £¨‘Ú
£¨‘Ú![]() Ķń≥§∂»xĶń»°÷Ķ∑∂őß «_____________£ģ
Ķń≥§∂»xĶń»°÷Ķ∑∂őß «_____________£ģ