题目内容
20．化简：$\sqrt{45}$=3$\sqrt{5}$．分析 把被开方数化为两数积的形式，再进行化简即可．
解答 解：原式=$\sqrt{5×9}$
=3$\sqrt{5}$．
故答案为：3$\sqrt{5}$．
点评 本题考查的是二次根式的性质与化简，熟知二次根式具有非负性是解答此题的关键．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
11．下列结论中，不正确的是（ ）
| A． | 射线有一个端点 | B． | 线段有两个端点 | ||
| C． | 两点确定一条直线 | D． | 两点之间，直线最短 |
如图，在△ABC中，∠ABC=50°，∠ACB=70°，延长CB至D，使BD=BA，延长BC至E，使CE=CA，则∠DAE=120°．
15．已知两条平行线被第三条直线所截，下列四个说法中正确的个数是（ ）
（1）同位角的平分线互相平行 （2）内错角的平分线互相平行
（3）同旁内角的平分线互相垂直 （4）邻补角的平分线互相垂直．
（1）同位角的平分线互相平行 （2）内错角的平分线互相平行
（3）同旁内角的平分线互相垂直 （4）邻补角的平分线互相垂直．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
5．计算$\sqrt{{{（\;-4\;）}^2}}$的结果是（ ）
| A． | 16 | B． | 4 | C． | 2 | D． | -4 |
12．
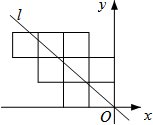八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）
八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）| A． | y=-x | B． | y=-$\frac{3}{4}$x | C． | y=-$\frac{3}{5}$x | D． | y=-$\frac{9}{10}$x |
9．已知y=$\sqrt{2x-5}$+$\sqrt{5-2x}$-3，则2xy的值为（ ）
| A． | $\frac{15}{2}$ | B． | 15 | C． | -$\frac{15}{2}$ | D． | -15 |