题目内容
已知二次函数y=x2–kx+k–1(k>2).
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若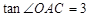 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与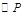 相离、相切、相交.
相离、相切、相交.
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若
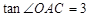 ,求抛物线的表达式;
,求抛物线的表达式;(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与
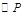 相离、相切、相交.
相离、相切、相交.(1)证明见解析;
(2)抛物线的表达式为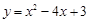 ;
;
(3)当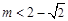 或
或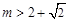 时,x轴与
时,x轴与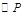 相离.
相离.
当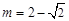 或
或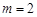 或
或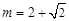 时,x轴与
时,x轴与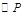 相切.
相切.
当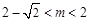 或
或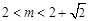 时,x轴与
时,x轴与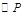 相交.
相交.
(2)抛物线的表达式为
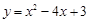 ;
;(3)当
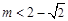 或
或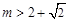 时,x轴与
时,x轴与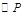 相离.
相离.当
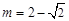 或
或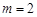 或
或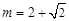 时,x轴与
时,x轴与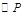 相切.
相切. 当
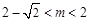 或
或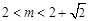 时,x轴与
时,x轴与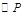 相交.
相交.试题分析:(1)要证明二次函数的图象与x轴都有两个交点,证明二次函数的判别式是正数即可解决问题;
(2)根据函数解析式求出A、B、C点坐标,再由
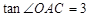 ,求出函数解析式;
,求出函数解析式;(3)先求出当
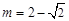 或
或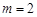 或
或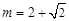 时,x轴与
时,x轴与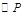 相切,再写出相离与相交.
相切,再写出相离与相交.试题解析:(1)∵
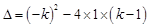
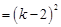 ,
,又∵
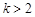 ,
,∴
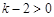 .
.∴
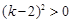 即
即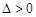 .
.∴抛物线y=x2–kx+k-1与x轴必有两个交点;
(2)∵抛物线y=x2–kx+k-1与x轴交于A、B两点,
∴令
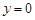 ,有
,有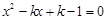 .
.解得:
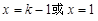 .
.∵
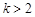 ,点A在点B的左侧,
,点A在点B的左侧,∴
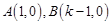 .
. ∵抛物线与y轴交于点C,
∴
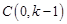 .
.∵在Rt
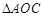 中,
中,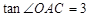 ,
,∴
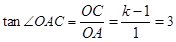 ,解得
,解得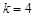 .
.∴抛物线的表达式为
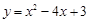 ;
;(3)解:当
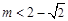 或
或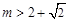 时,x轴与
时,x轴与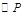 相离.
相离.当
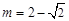 或
或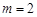 或
或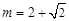 时,x轴与
时,x轴与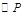 相切.
相切.当
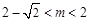 或
或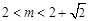 时,x轴与
时,x轴与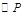 相交.
相交.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 向左平移一个单位,所得抛物线的表达式为: .
向左平移一个单位,所得抛物线的表达式为: . 向右平移
向右平移 个单位,所得新抛物线的函数解析式是( )
个单位,所得新抛物线的函数解析式是( ) ;
; ;
; ;
; .
.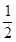 x2
x2 向右平移一个单位,所得函数解析式为 .
向右平移一个单位,所得函数解析式为 . 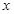 元,则降价后每件利润 元,每天可售出 件(用含
元,则降价后每件利润 元,每天可售出 件(用含


 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.