题目内容
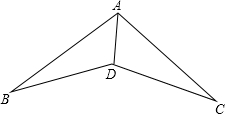
 如图,在△ABC中,BC>AC,在BC上取点D,使DC=AC,作CE⊥AD于E,点F是AB的中点,连结EF,则S△AEF:S四边形BDEF为( )
如图,在△ABC中,BC>AC,在BC上取点D,使DC=AC,作CE⊥AD于E,点F是AB的中点,连结EF,则S△AEF:S四边形BDEF为( )| A、3:4 | B、1:2 |
| C、1:3 | D、1:4 |
考点:三角形中位线定理,等腰三角形的性质,相似三角形的判定与性质
专题:
分析:由题意可推出△ADC为等腰三角形,CE⊥AD,因此E为AD的中点,所以EF为△ABD的中位线,即可计算出S△AEF:S四边形BDEF的值.
解答:解:∵DC=AC,
∴△ADC是等腰三角形,
∵CE⊥AD,
∴E为AD的中点(三线合一),
又∵点F是AB的中点,
∴EF为△ABD的中位线,
∴EF=
BD,△AFE∽△ABD,
∵S△AFE:S△ABD=1:4,
∴S△AFE:S四边形BDEF=1:3,
故选:C.
∴△ADC是等腰三角形,
∵CE⊥AD,
∴E为AD的中点(三线合一),
又∵点F是AB的中点,
∴EF为△ABD的中位线,
∴EF=
| 1 |
| 2 |
∵S△AFE:S△ABD=1:4,
∴S△AFE:S四边形BDEF=1:3,
故选:C.
点评:本题主要考查等腰三角形的判定和性质、三角形中位线的定义和性质、相似三角形的判定和性质,解题的关键在于求证EF为中位线,S△AFE:S△ABD=1:4.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )| A、∠B=∠C,BD=DC |
| B、∠ADB=∠ADC,BD=DC |
| C、∠B=∠C,∠BAD=∠CAD |
| D、BD=DC,AB=AC |
(a+3)(a2+9)(a-3)的计算结果( )
| A、a4+81 |
| B、-a4-81 |
| C、81-a4 |
| D、a4-81 |
已知△ABC≌△DEF,A与D,B与E,C与F分别为对应顶点,若AB=7cm,BC=5cm,AC=8cm,则EF=( )
| A、5cm | B、6cm |
| C、7cm | D、8cm |
 如图是一个正方体的展开图,标注了字母a的面是正方体的正面,如果正方体相对两个面上的整式的值相等,求整式(x+y)a的值.
如图是一个正方体的展开图,标注了字母a的面是正方体的正面,如果正方体相对两个面上的整式的值相等,求整式(x+y)a的值. 如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠6+∠1=180°;④∠4=∠7,其中能判断a∥b的条件有( )
如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠6+∠1=180°;④∠4=∠7,其中能判断a∥b的条件有( )