题目内容
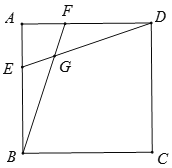
【题目】如图，在正方形ABCD中，AB＝a，E、F分别是AB、AD边上的点，BF，DE相交于点G，若AE＝
AB，AF＝AD，则四边形BCDG的面积是（ ）
A.
B.
C.
D.
【答案】C
【解析】
如图，以点B为坐标原点，BC所在直线为x轴，BA所在直线为y轴，建立平面直角坐标系，连接CG，过点G作GM⊥BC，GN⊥DC，分别求得直线BF和直线DE的解析式，从而可求得点G的坐标，则利用S四边形BCDG＝S△BCG+S△DCG，可求得答案．
如图，以点B为坐标原点，BC所在直线为x轴，BA所在直线为y轴，建立平面直角坐标系，连接CG，过点G作GM⊥BC，GN⊥DC
∵在正方形ABCD中，AB＝a，AE＝
AB，AF＝AD，
∴点B（0，0），E（0，
），F（
，a），D（a，a），
∴直线BF的解析式为：y＝3x，
设直线DE的解析式为：y＝kx+b，
将E（0，），D（a，a）代入得：
，
解得：
，
∴直线DE的解析式为y＝x+，
由
，
得：
，
∴G（
，
），
∴S四边形BCDG＝S△BCG+S△DCG
＝
BCGM+CDGN
＝（GM+GN）×a
∵GM＝yG＝，GN＝a﹣
＝，
∴S四边形BCDG＝×（+）×a＝
．
故选：C．
练习册系列答案
相关题目
【题目】为测量某特种车辆的性能，研究制定了行驶指数
，而
的大小与平均速度
和行驶路程
有关(不考虑其他因素)，由两部分的和组成，一部分与
成正比，另一部分与
成正比．在实验中得到了表格中的数据:
速度 |
|
|
路程 |
|
|
指数 |
|
|
（1）用含
和
的式子表示
;
（2）当行驶指数为
，而行驶路程为
时，求平均速度的值;
（3）当行驶路程为
时，若行驶指数值最大，求平均速度的值．
