Question

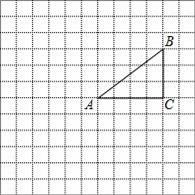
如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（，0），B（0，4），则点B₂₀₁₆的坐标为　　　　　　．

　

Answer 1

B₂₀₁₆（×10，4）．【考点】坐标与图形变化-旋转．

【专题】规律型．

【分析】根据图形和旋转规律可得出B_n点坐标的变换规律，结合三角形的周长，即可得出结论．

【解答】解：在直接三角形OAB中，OA=，OB=4，

由勾股定理可得：AB=，

△OAB的周长为：OA+OB+AB=+4+=10，

研究三角形旋转可知，当n为偶数时B_n在最高点，当n为奇数时B_n在x轴上，横坐标规律为：

，

∵2016为偶数，

∴B₂₀₁₆（×10，4）．

故答案为：．

【点评】本题考查的坐标与图形的变换，解题的关键是在变换中找到规律，结合图形得出结论．