题目内容
18.已知关于x的方程x2-(m+2)x+2m-1=0.(1)若此方程的一个根是1,请求出方程的另一个根;
(2)求证:方程恒有两个不相等的实数根.
分析 (1)把x=1代入原方程,先求出m的值,进而求出另一根;
(2)用m表示出方程根的判别式,进而根据非负数的性质作出判断.
解答 解:(1)当x=1时,1-(m+2)+2m-1=0,
解得m=2,
即原方程为x2-4x+3=0,
解得x1=1,x2=3,
故方程的另一个根为3;
(2)△=(m+2)2-4(2m-1)=m2-4m+8=(m-2)2+4>0,
则方程恒有两个不相等的实数根.
点评 本题考查了一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列等式成立的是( )
| A. | (-a2)3=a6 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+4)(a-4)=a2-4 |
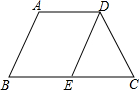 在梯形ABCD中AD∥BC,AB∥DE,且DE=DC,求证:梯形ABCD为等腰梯形.
在梯形ABCD中AD∥BC,AB∥DE,且DE=DC,求证:梯形ABCD为等腰梯形. 如图所示,A,B,C三点分别是张庄,李庄,赵庄,现在计划建一个文化娱乐站,使这个文化娱乐站到这三个村庄的距离相等,假如你是设计师,你怎样选择建文化娱乐站的地址?(请用尺规作图,不写作法,保留作图痕迹)
如图所示,A,B,C三点分别是张庄,李庄,赵庄,现在计划建一个文化娱乐站,使这个文化娱乐站到这三个村庄的距离相等,假如你是设计师,你怎样选择建文化娱乐站的地址?(请用尺规作图,不写作法,保留作图痕迹)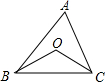 如图,O是△ABC内任意一点,连接OB、OC.
如图,O是△ABC内任意一点,连接OB、OC.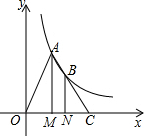 如图,点A,B在反比例函数y=$\frac{2}{x}(x>0)$的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,则S△ACM=2.
如图,点A,B在反比例函数y=$\frac{2}{x}(x>0)$的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,则S△ACM=2.