题目内容
 直线y=x-1与x轴交于点D,交函数y=
直线y=x-1与x轴交于点D,交函数y= (x>0)的图象于点B,直线y=2x交函数y=
(x>0)的图象于点B,直线y=2x交函数y= (x>0)的图象于点A,且OA=OB,则k=________.
(x>0)的图象于点A,且OA=OB,则k=________.
2
分析:由于点A在直线y=2x上,点B在直线y=x-1上,可设A点坐标为(t,2t),B点坐标为(a,a-1),(t>0,a>0),根据两点间的距离公式得到OA2=t2+(2t)2=5t2,OB2=a2+(a-1)2=2a2-2a+1,利用OA=OB得5t2=2a2-2a+1,再根据点A和点B在y= 的图象上得到k=t•2t=a(a-1),变形得t2=
的图象上得到k=t•2t=a(a-1),变形得t2= (a2-a),消去t得到5×
(a2-a),消去t得到5× (a2-a)=2a2-2a+1,解得a1=2,a2=-1(舍去),然后利用k=a(a-1)进行计算.
(a2-a)=2a2-2a+1,解得a1=2,a2=-1(舍去),然后利用k=a(a-1)进行计算.
解答:设A点坐标为(t,2t),B点坐标为(a,a-1),(t>0,a>0),
则OA2=t2+(2t)2=5t2,OB2=a2+(a-1)2=2a2-2a+1,
∵OA=OB,
∴5t2=2a2-2a+1,
又∵点A和点B在y= 的图象上,
的图象上,
∴k=t•2t=a(a-1),即t2= (a2-a),
(a2-a),
∴5× (a2-a)=2a2-2a+1,
(a2-a)=2a2-2a+1,
整理得a2-a-2=0,解得a1=2,a2=-1(舍去),
∴k=2×(2-1)=2.
故答案为2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.
分析:由于点A在直线y=2x上,点B在直线y=x-1上,可设A点坐标为(t,2t),B点坐标为(a,a-1),(t>0,a>0),根据两点间的距离公式得到OA2=t2+(2t)2=5t2,OB2=a2+(a-1)2=2a2-2a+1,利用OA=OB得5t2=2a2-2a+1,再根据点A和点B在y=
 的图象上得到k=t•2t=a(a-1),变形得t2=
的图象上得到k=t•2t=a(a-1),变形得t2= (a2-a),消去t得到5×
(a2-a),消去t得到5× (a2-a)=2a2-2a+1,解得a1=2,a2=-1(舍去),然后利用k=a(a-1)进行计算.
(a2-a)=2a2-2a+1,解得a1=2,a2=-1(舍去),然后利用k=a(a-1)进行计算.解答:设A点坐标为(t,2t),B点坐标为(a,a-1),(t>0,a>0),
则OA2=t2+(2t)2=5t2,OB2=a2+(a-1)2=2a2-2a+1,
∵OA=OB,
∴5t2=2a2-2a+1,
又∵点A和点B在y=
 的图象上,
的图象上,∴k=t•2t=a(a-1),即t2=
 (a2-a),
(a2-a),∴5×
 (a2-a)=2a2-2a+1,
(a2-a)=2a2-2a+1,整理得a2-a-2=0,解得a1=2,a2=-1(舍去),
∴k=2×(2-1)=2.
故答案为2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
相关题目
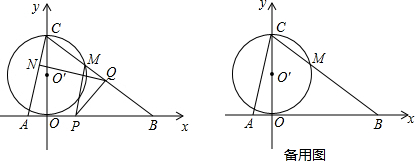
 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y=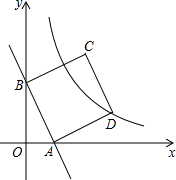 (2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=
(2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=