题目内容
【题目】在平面直角坐标系中,四边形ABCO是长方形,B点的坐标是(![]() ,3),C点的坐标是(
,3),C点的坐标是(![]() ,0)。若E是线段BC上的一点,长方形ABCO沿AE折叠后,B点恰好落在x轴上的P点处,求出此时P点和E点的坐标。
,0)。若E是线段BC上的一点,长方形ABCO沿AE折叠后,B点恰好落在x轴上的P点处,求出此时P点和E点的坐标。
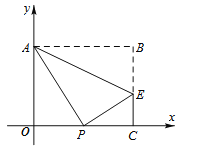
【答案】P点坐标为(![]() ,0);E点的坐标为(
,0);E点的坐标为(![]() ,1).
,1).
【解析】
首先根据勾股定理求出OP的长,然后设PE=BE=x,则EC=3x,进而在Rt△PCE中根据勾股定理列出方程求出BE的长,即可解决问题.
解:∵B点的坐标是(![]() ,3),
,3),
∴OC=AB=![]() ,BC=AO=3;
,BC=AO=3;
由题意得:AP=AB=![]() ,
,
∴![]() ,即P点坐标为(
,即P点坐标为(![]() ,0),
,0),
∴PC=![]()
设PE=BE=x,则EC=3x;
在Rt△PCE中,由勾股定理得:![]() ,即
,即![]() ,
,
解得:x=2,即BE=2,
∴EC=3x=1,
∴E点的坐标为(![]() ,1).
,1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目