ƒøƒ⁄»ð
‘⁄°˜CDE÷–£¨°œC=90°„£¨CD£¨CEµƒ≥§∑÷±Œ™m£¨n£¨«“DE•cosD=cotE£Æ£®1£©«Û÷§m2=n£ª
£®2£©»Ùm=2£¨≈◊ŒÔœþy=a£®x-m£©2+n”Î÷±œþy=3x+4Ωª”⁄A£®x1£¨y1£©∫ÕB£®x2£¨y2£©¡Ωµ„£¨«“°˜AOBµƒ√ʪ˝Œ™6£®OŒ™◊¯±Í‘≠µ„£©£¨«Ûaµƒ÷µ£ª
£®3£©»Ù «k2=
| n | m2 |
∑÷Œˆ£∫£®1£©”…“—÷™µƒ»˝Ω«∫Ø ˝µ√≥ˆDE•
=
£¨Õ∆≥ˆCD2=CEº¥ø…÷§√˜£Æ
£®2£©Ω‚πÿ”⁄∂˛¥Œ∫Ø ˝”Γª¥Œ∫Ø ˝◊È≥…µƒ∑Ω≥Ã◊È£¨¿˚”√“ª‘™∂˛¥Œ∑Ω≥Ã∏˘”Îœµ ˝µƒπÿœµº¥ø…«Û≥ˆABµƒæý¿Î£¨‘Ÿ∏˘æð÷±œþ”Îx÷·µƒΩªµ„ø…«Û≥ˆ°˜AOBµƒ∏þ£¨∏˘æð∆‰√ʪ˝º¥ø…«Û≥ˆaµƒ÷µ£Æ
£®3£©”…k2=
£¨c+l-b=0£¨ø…«Û≥ˆk°¢cµƒ÷µ£¨¥˙»Î≈◊ŒÔœþy=k£®x2+bx+c£©£¨‘Ÿ∏˘æð≈◊ŒÔœþy=k£®x2+bx+c£©”Îx÷·÷ª”–“ª∏ˆΩªµ„ø…«Û≥ˆ°˜µƒ÷µ£¨‘Ÿ¡Ìx=0£¨º¥ø…«Û≥ˆ≈◊ŒÔœþ”Îy÷·µƒΩªµ„◊¯±Í£¨∏˘æð°˜Ω¯––≈–∂œº¥ø…£Æ
| CD |
| DE |
| CE |
| CD |
£®2£©Ω‚πÿ”⁄∂˛¥Œ∫Ø ˝”Γª¥Œ∫Ø ˝◊È≥…µƒ∑Ω≥Ã◊È£¨¿˚”√“ª‘™∂˛¥Œ∑Ω≥Ã∏˘”Îœµ ˝µƒπÿœµº¥ø…«Û≥ˆABµƒæý¿Î£¨‘Ÿ∏˘æð÷±œþ”Îx÷·µƒΩªµ„ø…«Û≥ˆ°˜AOBµƒ∏þ£¨∏˘æð∆‰√ʪ˝º¥ø…«Û≥ˆaµƒ÷µ£Æ
£®3£©”…k2=
| n |
| m2 |
Ω‚¥£∫£®1£©÷§√˜£∫”…DE•cosD=cotE£¨”–DE•
=
£Æ
°ýCD2=CE£¨
°ým2=n£Æ
£®2£©Ω‚£∫”…“‚µ√
£¨
º¥ax2-£®4a+3£©x+4a=0
°ýx1+x2=
£¨x1x2=4£Æ
°ý|x1-x2|=
=
=
=
°ý|AB|=
£Æ
”÷÷±œþy=3x+4”Îy÷·Ωª”⁄M£®0£¨4£©£¨”Îx÷·Ωª”⁄N£®-
£¨0£©£Æ
…ËOH=h¥π÷±”⁄MN£¨
‘Úh=
°þ
•
•
=6£¨
°ý
=3|a|£Æ
°ýa=3ªÚa=-
£Æ
£®3£©°þk2=
£¨c+l-b=0£¨
°ýk2=
=
=1£¨c+1-b=0£¨c=b-1£¨
≈◊ŒÔœþy=k£®x2+bx+c£©ø…ªØŒ™y=x2+bx+b-1£¨
°þ≈◊ŒÔœþ”Îx÷·÷ª”–“ª∏ˆΩªµ„£¨‘⁄‘≠µ„µƒ”“≤ý£¨
°ý°˜=b2-4£®b-1£©=b2-4b+4=0£¨º¥b-1=
£æ0
¡Óx=0£¨‘Úy=b-1=
£æ0£¨
π ≈◊ŒÔœþ”Îy÷·µƒΩªµ„‘⁄y÷·µƒ’˝∞Î÷·£Æ
| CD |
| DE |
| CE |
| CD |
°ýCD2=CE£¨
°ým2=n£Æ
£®2£©Ω‚£∫”…“‚µ√
|
º¥ax2-£®4a+3£©x+4a=0
°ýx1+x2=
| 4a+3 |
| a |
°ý|x1-x2|=
| (x1+x2)2-4x1x2 |
=
|
|
| ||
| |a| |
°ý|AB|=
|
”÷÷±œþy=3x+4”Îy÷·Ωª”⁄M£®0£¨4£©£¨”Îx÷·Ωª”⁄N£®-
| 4 |
| 3 |
…ËOH=h¥π÷±”⁄MN£¨
‘Úh=
| 4 | ||
|
°þ
| 1 |
| 2 |
| ||
| |a| |
| 4 | ||
|
°ý
| 24a+9 |
°ýa=3ªÚa=-
| 1 |
| 3 |
£®3£©°þk2=
| n |
| m2 |
°ýk2=
| n |
| m2 |
| 4 |
| 22 |
≈◊ŒÔœþy=k£®x2+bx+c£©ø…ªØŒ™y=x2+bx+b-1£¨
°þ≈◊ŒÔœþ”Îx÷·÷ª”–“ª∏ˆΩªµ„£¨‘⁄‘≠µ„µƒ”“≤ý£¨
°ý°˜=b2-4£®b-1£©=b2-4b+4=0£¨º¥b-1=
| b2 |
| 4 |
¡Óx=0£¨‘Úy=b-1=
| b2 |
| 4 |
π ≈◊ŒÔœþ”Îy÷·µƒΩªµ„‘⁄y÷·µƒ’˝∞Î÷·£Æ
µ„∆¿£∫±æÂøº≤ȵƒ «»ÒΩ«»˝Ω«∫Ø ˝µƒ∂®“£¨∂˛¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿµ„º∞“ª‘™∂˛¥Œ∑Ω≥Ã∏˘”Îœµ ˝µƒπÿœµ£¨…ʺ∞√ÊΩœπ„£¨µ´ƒ—∂» ÷–£Æ

¡∑œ∞≤·œµ¡–¥∞∏
œýπÿƒø
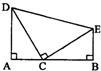 26°¢»ÁÕº‘⁄°˜CDE÷–£¨°œDCE=90°„£¨DC=CE£¨DA°ÕAB”⁄A£¨EB°ÕAB”⁄B£¨ ‘≈–∂œAB”ÎAD£¨BE÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢÷§√˜£Æ
26°¢»ÁÕº‘⁄°˜CDE÷–£¨°œDCE=90°„£¨DC=CE£¨DA°ÕAB”⁄A£¨EB°ÕAB”⁄B£¨ ‘≈–∂œAB”ÎAD£¨BE÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢÷§√˜£Æ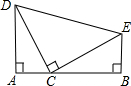 “—÷™£∫»ÁÕºÀ˘ 棨‘⁄°˜CDE÷–£¨°œDCE=90°„£¨CD=CE£¨DA°ÕAB”⁄A£¨EB°ÕAB”⁄B
“—÷™£∫»ÁÕºÀ˘ 棨‘⁄°˜CDE÷–£¨°œDCE=90°„£¨CD=CE£¨DA°ÕAB”⁄A£¨EB°ÕAB”⁄B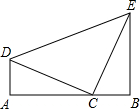 Œ™A°¢B£¨ ‘Àµ√˜AC=BEµƒ¿Ì”…£Æ
Œ™A°¢B£¨ ‘Àµ√˜AC=BEµƒ¿Ì”…£Æ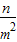 £¨c+l-b=0£¨≈◊ŒÔœþy=k£®x2+bx+c£©”Îx÷·÷ª”–“ª∏ˆΩªµ„‘⁄‘≠µ„µƒ”“≤ý£¨ ‘≈–∂œ≈◊ŒÔœþ”Îy÷·µƒΩªµ„‘⁄y÷·µƒ’˝∞Î÷·ªπ «∏∫∞Î÷·£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
£¨c+l-b=0£¨≈◊ŒÔœþy=k£®x2+bx+c£©”Îx÷·÷ª”–“ª∏ˆΩªµ„‘⁄‘≠µ„µƒ”“≤ý£¨ ‘≈–∂œ≈◊ŒÔœþ”Îy÷·µƒΩªµ„‘⁄y÷·µƒ’˝∞Î÷·ªπ «∏∫∞Î÷·£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ