题目内容
15.⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB和CD的距离是7cm或1cm.分析 作OE⊥AB于E,交CD于F,连结OA、OC,如图,根据平行线的性质得OF⊥CD,再利用垂径定理得到AE=BE=$\frac{1}{2}$AB=4cm,CF=DF=$\frac{1}{2}$CD=3cm,接着根据勾股定理,在Rt△OAE中计算出OE=3cm,在Rt△OCF中计算出OF=4cm,然后分类讨论:当圆心O在AB与CD之间时,EF=OF+OE;当圆心O不在AB与CD之间时,EF=OF-OE.
解答 解: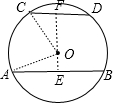 作OE⊥AB于E,交CD于F,连结OA、OC,如图,
作OE⊥AB于E,交CD于F,连结OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=$\frac{1}{2}$AB=4cm,CF=DF=$\frac{1}{2}$CD=3cm,
在Rt△OAE中,∵OA=5cm,AE=4cm,
∴OE=3cm,
在Rt△OCF中,∵OC=5cm,CF=3cm,
∴OF=4cm,
当圆心O在AB与CD之间时,EF=OF+OE=3+4+=7cm;
当圆心O不在AB与CD之间时,EF=OF-OE=4-3=1cm;
即AB和CD之间的距离为7cm或1cm.
故答案为7cn或1cm.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.学会运用分类讨论的思想解决数学问题.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
20. 把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )
把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )
 把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )
把两块三角板按如图所示那样拼在一起,则∠ABC的补角等于( )| A. | 135° | B. | 60° | C. | 45° | D. | 120° |
7.下列各组数中,不是互为相反意义的量的是( )
| A. | 收入200元与支出200元 | B. | 上升7米和下降8米 | ||
| C. | 超过0.05mm与不足0.05mm | D. | 增多2件与减少2升 |
5.下列各组中的两项,不是同类项的是( )
| A. | 2x2y与-2x2y | B. | x3与3x | C. | -3ab2c3与c3b2a | D. | 1与-8 |
