题目内容
 己知,如图,在Rt△ABC中,∠C=90°,以Rt△ABC的三边为斜边分别向外作三个等腰直角三角形,其中∠H、∠E、∠F是直角,若斜边AB=3,则图中阴影部分的面积为
己知,如图,在Rt△ABC中,∠C=90°,以Rt△ABC的三边为斜边分别向外作三个等腰直角三角形,其中∠H、∠E、∠F是直角,若斜边AB=3,则图中阴影部分的面积为
- A.1
- B.2
- C.

- D.

C
分析:在直角△ABC中,∠C=90°,AB2=AC2+BC2,即可求证:阴影部分面积△ACH和△BCF的面积之和为△ABE的面积,即阴影部分面积为2倍的△ABE的面积,根据此等量关系即可求解.
解答:在直角△ABC中,∠C=90°,∴AB2=AC2+BC2,
根据等腰直角三角形面积计算方法,△AEB的面积为 ×AB•
×AB• AB=
AB=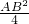 ,
,
△AHC的面积为 ×AC•
×AC• AC=
AC=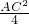 ,
,
△BCF的面积为 ×BC•
×BC• BC=
BC=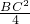 ,
,
∴阴影部分面积为 (AB2+AC2+BC2)=
(AB2+AC2+BC2)= AB2,
AB2,
∵AB=3,
∴阴影部分面积为 ×32=
×32= .
.
故选C.
点评:本题考查了直角三角形中勾股定理的运用,考查了等腰直角三角形面积的计算,本题中求△AEB的面积、△AHC的面积、△BCF的面积并用AB表示是解题的关键.
分析:在直角△ABC中,∠C=90°,AB2=AC2+BC2,即可求证:阴影部分面积△ACH和△BCF的面积之和为△ABE的面积,即阴影部分面积为2倍的△ABE的面积,根据此等量关系即可求解.
解答:在直角△ABC中,∠C=90°,∴AB2=AC2+BC2,
根据等腰直角三角形面积计算方法,△AEB的面积为
 ×AB•
×AB• AB=
AB=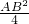 ,
,△AHC的面积为
 ×AC•
×AC• AC=
AC=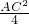 ,
,△BCF的面积为
 ×BC•
×BC• BC=
BC=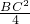 ,
,∴阴影部分面积为
 (AB2+AC2+BC2)=
(AB2+AC2+BC2)= AB2,
AB2,∵AB=3,
∴阴影部分面积为
 ×32=
×32= .
.故选C.
点评:本题考查了直角三角形中勾股定理的运用,考查了等腰直角三角形面积的计算,本题中求△AEB的面积、△AHC的面积、△BCF的面积并用AB表示是解题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
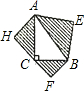 己知,如图,在Rt△ABC中,∠C=90°,以Rt△ABC的三边为斜边分别向外作三个等腰直角三角形,其中∠H、∠E、∠F是直角,若斜边AB=3,则图中阴影部分的面积为( )
己知,如图,在Rt△ABC中,∠C=90°,以Rt△ABC的三边为斜边分别向外作三个等腰直角三角形,其中∠H、∠E、∠F是直角,若斜边AB=3,则图中阴影部分的面积为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
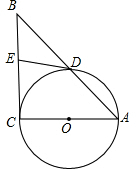 己知:如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙0交AB于点D.
己知:如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙0交AB于点D. 己知:如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙0交AB于点D.
己知:如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙0交AB于点D. ,AC=6,求线段BD的长.
,AC=6,求线段BD的长. ,AC=6,求线段BD的长.
,AC=6,求线段BD的长.