题目内容
如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则BD的长为( )

A.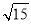 B.
B.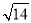 C.3
C.3 D.2
D.2
B.
【解析】
试题分析:以A为圆心,AB长为半径作圆,延长BA交⊙A于F,连接DF.

∵DC∥AB,
∴
∴DF=CB=1,BF=2+2=4,
∵FB是⊙A的直径,
∴∠FDB=90°,
∴BD=
故选B.
考点:勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则BD的长为( )

A.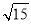 B.
B.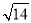 C.3
C.3 D.2
D.2
B.
【解析】
试题分析:以A为圆心,AB长为半径作圆,延长BA交⊙A于F,连接DF.

∵DC∥AB,
∴
∴DF=CB=1,BF=2+2=4,
∵FB是⊙A的直径,
∴∠FDB=90°,
∴BD=
故选B.
考点:勾股定理.

 名校课堂系列答案
名校课堂系列答案