题目内容
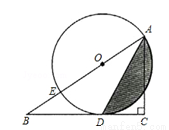
如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为 .
.

(1)求证:DC是⊙O的切线;
(2)如果AC∥BD,证明四边形ACDB是平行四边形,并求其周长.
(1)证明见解析;(2)证明见解析;2 +2
+2 .
.
【解析】
试题分析:(1)连接OC,由于∠A=30°,利用圆周角定理可知∠BOC=60°,而∠BDC=30°,利用三角形内角和定理可求∠DCO=90°,从而可证CD是⊙的切线;
(2)由于AC∥BD,那么∠ABO=∠BAC=30°,而∠BDC=30°,等量代换可得∠ABO=∠BDC,根据平行线的判定可知AB∥CD,于是可证四边形ABDC是平行四边形,在Rt△OCD中,由于∠BDC=30°,OC= ,可知OD=2OC=2
,可知OD=2OC=2 ,易求BD=
,易求BD= ,再利用特殊三角函数值可求CD=
,再利用特殊三角函数值可求CD= ,进而可求平行四边形ABCD的周长.
,进而可求平行四边形ABCD的周长.
试题解析:(1)证明:连接OC,如图

∵∠A=30°,
∴∠BOC=60°
又∵∠BDC=30°,
∴∠DCO=90°,
∴CD是⊙O的切线;
(2)证明:∵AC∥BD,
∴∠ABO=∠BAC=30°,
又∵∠BDC=30°,
∴∠ABO=∠BDC,
∴AB∥CD,
∴四边形ABDC是平行四边形,
在Rt△CDO中,
∵∠BDC=30°,OC= ,
,
∴OD=2OC=2 ,CD=
,CD= OC=
OC= ,
,
∴DB=OD-OB= ,
,
∴平行四边形ABDC的周长=2(DB+DC)=2( +
+ )=2
)=2 +2
+2 .
.
考点:1.切线的判定与性质;2.平行四边形的判定与性质.

练习册系列答案
相关题目
 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )



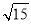 B.
B.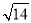 C.3
C.3 D.2
D.2

 ,那么截成的两段铜丝的长度差应是 m.
,那么截成的两段铜丝的长度差应是 m.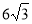 .
.