题目内容
如图，已知：在△ABC中，∠A=80°，BD=BE，CD=CF．那么∠EDF=________．
50°
分析：等腰三角形中等边对等角．根据此性质可求出∠EDF的度数．
解答：∵∠A=80°，
∴∠B+∠C=180°-80°=100°，
∵BD=BE，CD=CF，
∴∠EDB+∠FDC=（360°-100°）÷2=130°．
∴∠EDF=180°-130°=50°．
故答案为：50°．
点评：本题考查等腰三角形的性质，等边对等角，以及三角形的内角和为180°和平角的概念．
分析：等腰三角形中等边对等角．根据此性质可求出∠EDF的度数．
解答：∵∠A=80°，
∴∠B+∠C=180°-80°=100°，
∵BD=BE，CD=CF，
∴∠EDB+∠FDC=（360°-100°）÷2=130°．
∴∠EDF=180°-130°=50°．
故答案为：50°．
点评：本题考查等腰三角形的性质，等边对等角，以及三角形的内角和为180°和平角的概念．
练习册系列答案
相关题目
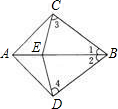
如图，已知：在Rt△ABC中，∠C=90°，E为AB的中点，且DE⊥AB于E，若∠CAD：∠DAB=1﹕2，求∠B的度数．
