题目内容
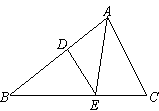
如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．
求证：CD=AF．
证明：∵FC∥AB，
∴∠DAC=∠ACF，∠ADF=∠DFC．
又∵AE=CE，
∴△ADE≌△CFE（AAS）．
∴DE=EF．
∵AE=CE，
∴四边形ADCF为平行四边形．
∴CD=AF．
分析：要证CD=AF，需证四边形ADCF为平行四边形，需再证DE=EF，可经过证明△ADE≌△CFE求得．
点评：此题主要考查平行四边形的判定和性质以及全等三角形的判定．熟练掌握性质定理和判定定理是解题的关键．
∴∠DAC=∠ACF，∠ADF=∠DFC．
又∵AE=CE，
∴△ADE≌△CFE（AAS）．
∴DE=EF．
∵AE=CE，
∴四边形ADCF为平行四边形．
∴CD=AF．
分析：要证CD=AF，需证四边形ADCF为平行四边形，需再证DE=EF，可经过证明△ADE≌△CFE求得．
点评：此题主要考查平行四边形的判定和性质以及全等三角形的判定．熟练掌握性质定理和判定定理是解题的关键．
练习册系列答案
相关题目
2、如图所示，D为AB边上一点，AD：DB=3：4，DE∥AC交BC于点E，则S△BDE：S△AEC等于（ ）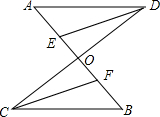
已知如图所示，O为AB、CD的中点，AE=BF，你从图中可以找到全等三角形共（ ）
