Question

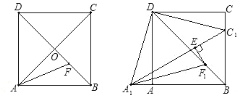
【题目】如图，在正方形中，对角线与相交于点，平分，交于点．

求证：；

点、点分别同时从、两点出发，以相同的速度运动相同的时间后同时停止，如图，平分，交于点，过点作，垂足为，请猜想，与三者之间的数量关系，并证明你的猜想；

在的条件下，当，时，求的长．

Answer 1

【答案】证明见解析； ；．

【解析】

（1）过作于，根据角平分线的性质可以得到OF=FG，然后利用正方形的性质可以得到条件证明Rt△AOF≌Rt△AGF，再根据全等三角形的性质与等腰直角三角形的性质可以证明题目结论．（2）过作，过作，可知四边形是矩形，根据，可知四边形是正方形，进而得：，所以是三角形的内心，根据内心的性质即可求出答案.（3）由F1是内心，E1、G1、H1是切点可知，可求出，根据勾股定理求出AB的长，即可求出BD的长.

过作于，

∵平分，，，

∴，

∵，，，

∴，

∴，

直角三角形中，，

∴，

∴，

∴．

过作，过作，则四边形是矩形．

由可得，因此四边形是正方形．

∴，

即：是三角形的内心，

∴EF1=（A1B+BC1-A1C1） 2…①

∵，而，

∴，

因此①式可写成：，

即 AB-EF1=A1C

解：由得，是三角形的内心，且、、都是切点．

∴，

如果设，

，

∴，

在直角三角形中，根据勾股定理有，

即：，

解得，

∴．