题目内容
计算：①已知tanA=
，求sinA，cosA．②cos45°•tan45°+
tan30°-2cos60°•sin45°．
解：①∵tanA=，∴
=，
设a=4x，b=3x，则c=5x，
∴sinA=
=
=
，
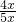cosA=
=
=
；
②原式=
×1+×
-2×
×
=+1-
=1．
分析：①根据正切的定义，设a=4x，b=3x，则c=5x，再由正弦和余弦的定义求得sinA，cosA；
②由特殊角的三角函数值求解即可．
点评：本题考查了特殊角的三角函数和同角三角函数的关系，是基础知识比较简单．
，∴=，设a=4x，b=3x，则c=5x，
∴sinA=
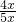==，cosA=
==；②原式=
×1+×-2××=
+1-=1．
分析：①根据正切的定义，设a=4x，b=3x，则c=5x，再由正弦和余弦的定义求得sinA，cosA；
②由特殊角的三角函数值求解即可．
点评：本题考查了特殊角的三角函数和同角三角函数的关系，是基础知识比较简单．
练习册系列答案
相关题目
＝________，已知tanA＝0.457 8，则∠A＝________．
，求sinA，cosA．②cos45°•tan45°+
tan30°-2cos60°•sin45°．