题目内容
【题目】如果两个一次函数![]() 和
和![]() 满足
满足![]() ,那么称这两个一次函数为“平行一次函数”.
,那么称这两个一次函数为“平行一次函数”.
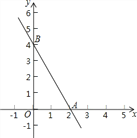
如图,已知函数![]() 的图象与x轴、y轴分别交于A、B两点,一次函数
的图象与x轴、y轴分别交于A、B两点,一次函数![]() 与
与![]() 是“平行一次函数”
是“平行一次函数”
![]() 若函数
若函数![]() 的图象过点
的图象过点![]() ,求b的值;
,求b的值;
![]() 若函数
若函数![]() 的图象与两坐标轴围成的三角形和
的图象与两坐标轴围成的三角形和![]() 构成位似图形,位似中心为原点,位似比为1:2,求函数
构成位似图形,位似中心为原点,位似比为1:2,求函数![]() 的表达式.
的表达式.
【答案】(1)7;(2)![]() ,
, ![]()
【解析】试题分析:(1)根据平行一次函数的定义可知: ![]() 再利用待定系数法求出
再利用待定系数法求出![]() 的值即可;
的值即可;
(2)根据位似比为1:2可知:函数![]() 与两坐标的交点坐标,再利用待定系数法求出函数
与两坐标的交点坐标,再利用待定系数法求出函数![]() 的表达式.
的表达式.
试题解析: ![]() 由已知得:
由已知得: ![]() ,把点
,把点![]() 和
和![]() 代入
代入![]() 中得:
中得: ![]() ,
, ![]() ;
;
![]() 根据位似比为1:2得:函数
根据位似比为1:2得:函数![]() 的图象有两种情况:
的图象有两种情况:
![]() 不经过第三象限时,过
不经过第三象限时,过![]() 和
和![]() ,这时表达示为:
,这时表达示为: ![]() ;
;
![]() 不经过第一象限时,过
不经过第一象限时,过![]() 和
和![]() ,这时表达示为:
,这时表达示为: ![]() ;
;


练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目