题目内容
如图，扇形OAB的圆心角为90°，分别以OA、OB为直径在扇形内作半圆，P和Q分别表示两个阴影部分，试判定P与Q面积的大小关系．
解：∵扇形OAB的圆心角为90°，假设扇形半径为a，∴扇形面积为：
=
，半圆面积为：
×π×（
）2=
，∴SQ+SM =SM+SP=
，∴SQ=SP，
即P与Q面积的大小相等．
分析：假设出扇形半径，再表示出半圆面积，以及扇形面积，进而即可表示出两部分阴影面积．
点评：此题主要考查了扇形面积求法，根据已知得出半圆面积以及扇形面积是解题关键．
练习册系列答案
相关题目
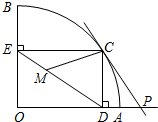如图，扇形OAB的半径OA=r，圆心角∠AOB=90°，点C是
（2012•珠海三模）如图：扇形OAB的圆心角∠AOB=120°，半径OA=6cm，
