Question

【题目】如图，在平面直角系xOy中，直线AB交x轴正半轴于点A，交y轴负半轴于点B，B点的坐标为B（0，﹣6），点C在线段OA上，将△ABC沿直线BC翻折，点A与y轴上的点D（0，4），恰好重合．

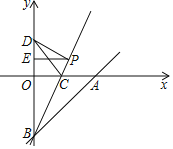
（1）求A点、C点的坐标；

（2）在y轴是否存在一点H，使得△HAB和△ABC的面积相等？若存在，求出满足条件的点H的坐标；若不存在，请说明理由

（3）已知点E（0，3），P是直线BC上一动点（P不与B重合），连接PD、PE，求△PDE周长的最小值，并求出此BP长．

Answer 1

【答案】（1）A（8，0），C（3，0）；（2）存在，（0，﹣），（0，﹣）；（3）△PDE的周长的最小值+1，.

【解析】

（1）由折叠的性质得BD＝AB＝10，AC＝DC，由勾股定理可求AO＝8，AC＝5，即可求点A，点C坐标；

（2）△HAB和△ABC的面积相等，则点H在直线m、n与y轴的交点上，求出直线m、n的表达式即可求解；

（3）连接AE交BC于点P，则此时△PDE的周长取得最小值，即可求解．

解：（1）∵B（0，﹣6），D（0，4），

∴BD＝10，

∵将△ABC沿直线BC翻折，

∴BD＝AB＝10，AC＝DC，

∴AO＝＝＝8，

∴点A（8，0）

∵CD2＝DO2+CO2，

∴AC2＝16+（8﹣AC）2，

∴AC＝5，

∴CO＝3，

∴点C（3，0）

（2）过点C作直线m∥AB，

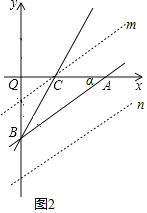
∵B点的坐标为B（0，﹣6），点A坐标（8，0），

∴直线AB的解析式为：y＝x﹣6

∵直线m∥AB，

∴设直线m的解析式为：y＝x+b，且过点C，

∴0＝×3+b，

∴b＝﹣

直线m的解析式为：y＝x﹣，

在直线AB下方与直线m等距离处作直线n，

则直线n的表达式为：y＝x﹣，

∵△HAB和△ABC的面积相等，则点H在直线m、n与坐标轴的交点上，

∴点H坐标为（0，﹣），（0，﹣）；

（3）∵点A与点D关于BC对称，

∴连接AE交BC于点P，

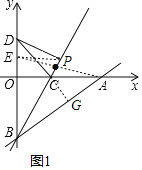
则此时△PDE的周长取得最小值，

∵点A（8，0），点E（0，3）

∴AE＝

∴△PDE的周长的最小值＝DE+DP+PE＝+1

由点E、A的坐标，同理可得：直线AE的表达式为：y＝﹣x+3，

同理直线BC的表达式为：y＝2x﹣6，

∴

∴

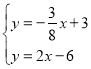
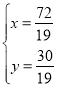
∴点P（，）

∵点B（0，﹣6）

∴BP＝.