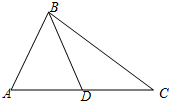
题目内容
已知△ABC中，点D为直线AB上一点，过点D作DE∥BC交直线AC于点E，若BD：BA=3：5，BC=10，则DE=
4或16
4或16
．分析：首先根据题目的条件画出图形，再根据相似三角形的判定和性质解答即可，注意图形不唯一．
解答：解：
当DE在三角形ABC的内部时如图①，
∵DE∥BC，
∴△ADE∽△ABC，
∴
=
，
∵BD：BA=3：5，BC=10，
∴
=
，
∴DE=4，
当DE在三角形ABC的外部时如图②，
同理可求出DE=16．
故答案为：4或16．
当DE在三角形ABC的内部时如图①，∵DE∥BC，
∴△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| BC |
∵BD：BA=3：5，BC=10，
∴
| 2 |
| 5 |
| DE |
| 10 |
∴DE=4，
当DE在三角形ABC的外部时如图②，
同理可求出DE=16．
故答案为：4或16．
点评：本题考查了相似三角形的性质和判定，解题的关键是正确的画出图形，并且注意分类讨论数学思想的运用．
练习册系列答案
相关题目
如图，已知△ABC中，点D为边AC的中点，设
19、如图，已知△ABC中，点F是BC的中点，DE∥BC，则DG和GE有怎样的关系？请你说明理由．
22、如图，已知△ABC中，点D、E在BC上，AB=AC，AD=AE．请说明BD=CE的理由．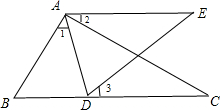
如图所示，已知△ABC中，点D为BC边上一点，∠1=∠2=∠3，AC=AE，