Question

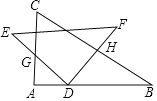
【题目】一副三角板（△ABC与△DEF）如图放置，点D在AB边上滑动，DE交AC于点G，DF交BC于点H，且在滑动过程中始终保持DG＝DH，若AC＝2，则△BDH面积的最大值是（ ）

A.3B.3C.D.

Answer 1

【答案】C

【解析】

解直角三角形求得AB=2，作HM⊥AB于M，证得△ADG≌△MHD，得出AD=HM，设AD=x，则BD=2x，根据三角形面积公式即可得到S△BDHBDADx(2x)(x)2，根据二次函数的性质即可求得．

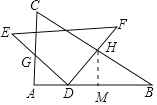
如图，作HM⊥AB于M．

∵AC=2，∠B=30°，

∴AB=2，

∵∠EDF=90°，

∴∠ADG+∠MDH=90°．

∵∠ADG+∠AGD=90°，

∴∠AGD=∠MDH．

∵DG=DH，∠A=∠DMH=90°，

∴△ADG≌△MHD(AAS)，

∴AD=HM，

设AD=x，则HM=x，BD=2x，

∴S△BDHBDADx(2x)(x)2，

∴△BDH面积的最大值是．

故选：C．