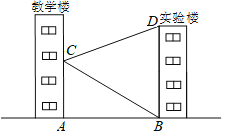
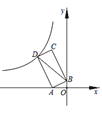
题目内容
【题目】观察下列图形:

(1)可知tanα=![]() ,tanβ=
,tanβ=![]() ,用“画图法”求tan(α+β)的值,具体解法如下:
,用“画图法”求tan(α+β)的值,具体解法如下:
第一步:如图1所示,构造符合题意两个“背靠背”的直角三角形;
第二步:如图2所示,将图1中所有数据同比例扩大3倍;
第三步:如图3所示,依托中间的Rt△ABD的各顶点构造“水平﹣﹣竖直辅助线”,构造出“一线三直角”基本相似型,并补成矩形ACEF;由图可知tan(α+β)= .
(2)依据(1)的方法,已知tanα=![]() ,tanβ=
,tanβ=![]() ,用“画图法”求tan(α+β)的值.
,用“画图法”求tan(α+β)的值.
(3)扩展延伸,已知tanα=![]() ,tanβ=
,tanβ=![]() ,直接写出tan(α﹣β)= .
,直接写出tan(α﹣β)= .
【答案】(1)1;(2)见解析,![]() ;(3)
;(3)![]()
【解析】
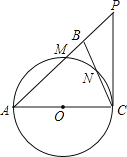
(1)按照提示的方法画矩形ACEF,AB⊥BD,由△ABC∽△BDE,可得出DE=1,BE=2,CE=5,DF=5,得tan(α+β)=1;
(2)如图4,四边形ABCD是矩形,点E、F分别在CD、AD边上,tanα=![]() ,tanβ=
,tanβ=![]() ,根据勾股定理和相似三角形性质易求得tan(α+β)=
,根据勾股定理和相似三角形性质易求得tan(α+β)=![]() ;
;
(3)如图5,矩形ABCD中,AB=CD=17,AD=BC=52,CE=13,DE=4,DF=1,∠AFB=α=∠CBF,∠CBE=β,∠EBF=α﹣β,根据勾股定理和相似三角形性质易求得:tan(α﹣β)=![]() .
.
解:(1)如图3,
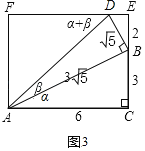
∵四边形ACEF是矩形,
∴∠C=∠E=∠F=90°,AC∥EF,EF=AC,AF=CE,∠CAB+∠ABC=90°,
∵∠ABD=90°,
∴∠DBE+∠ABC=90°,
∴∠CAB=∠DBE,
∴△ABC∽△BDE,
∴![]() =
=![]() =
=![]() =
=![]() ,设DE=m,BE=2m,
,设DE=m,BE=2m,
∵DE2+BE2=BD2,即:m2+(2m)2=![]() ,解得m1=1,m2=﹣1(舍去),
,解得m1=1,m2=﹣1(舍去),
∴DE=1,BE=2,CE=BC+BE=3+2=5,DF=EF﹣DE=6﹣1=5,
∵AC//EF,
∴∠ADF=∠CAD=α+β,
∴tan(α+β)=tan∠ADF=![]() =1,
=1,
故答案为:1.
(2)如图4,
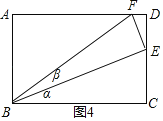
四边形ABCD是矩形,点E、F分别在CD、AD边上,令CE=2,BC=6,
∵∠ACE=90°,
由勾股定理得:BE=![]() =
=![]() =2
=2![]() ,
,
设∠CBE=α,∠EBF=β,EF=![]() ,∠BEF=90°,
,∠BEF=90°,
∴tanα=![]() =
=![]() =
=![]() ,tanβ=
,tanβ=![]() =
=![]() =
=![]() ,
,
∵∠BEC+∠CBE=90°,∠BEC+∠DEF=90°,
∴∠DEF=∠CBE=α,
∴tan∠DEF=tanα=![]() =
=![]() ,
,
设DF=n,DE=3n,则n2+(3n)2=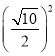 ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴DF=![]() ,DE=
,DE=![]() ,
,
∴AB=CD=CE+DE=2+![]() =
=![]() ,AF=AD﹣DF=6﹣
,AF=AD﹣DF=6﹣![]() =
=![]() ,
,
∵AD//BC,
∴∠AFB=∠CBF=α+β,
∴tan(α+β)=tan∠AFB=![]() =
=![]() =
=![]() ;
;
(3)如图5,
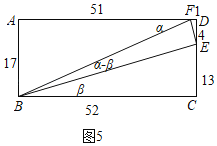
矩形ABCD中,令AB=CD=17,AD=BC=52,CE=13,DE=4,DF=1,
∠AFB=α=∠CBF,∠CBE=β,∠EBF=α﹣β,
则tanα=![]() ,tanβ=
,tanβ=![]() ,BE=
,BE=![]() =13
=13![]() ,EF=
,EF=![]() =
=![]() ,
,
∵tan∠DEF=![]() =tanβ,
=tanβ,
∴∠DEF=β=∠CBE,
∵∠CBE+∠BEC=90°,
∴∠DEF+∠BEC=90°,
∴∠BEF=90°,
∴tan(α﹣β)=![]() =
=![]() =
=![]() ,
,
故答案为:![]() .
.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?