题目内容
 如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上运动(与A、B两点不重合),如果∠P=46°,那么∠ACB的度数是________.
如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上运动(与A、B两点不重合),如果∠P=46°,那么∠ACB的度数是________.
72°
分析:连接OA、OB.根据切线的性质,得到∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB,再进一步根据圆周角定理求解即可.
解答: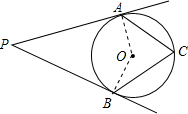 解:连接OA、OB.
解:连接OA、OB.
∵PA、PB是⊙O的切线,切点分别为A、B,
∴∠OAP=∠OBP=90°(切线的性质).
∵∠P=46°(已知),
∴∠AOB=180°-∠P=134°(四边形的内角和定理),
∴∠ACB= ∠AOB=72°(同弧所对的圆周角是所对的圆心角的一半).
∠AOB=72°(同弧所对的圆周角是所对的圆心角的一半).
故答案是:72°.
点评:综合运用了切线的性质定理、四边形的内角和定理以及圆周角定理.连接OA与OB,熟练运用性质及定理是解本题的关键.
分析:连接OA、OB.根据切线的性质,得到∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB,再进一步根据圆周角定理求解即可.
解答:
 解:连接OA、OB.
解:连接OA、OB.∵PA、PB是⊙O的切线,切点分别为A、B,
∴∠OAP=∠OBP=90°(切线的性质).
∵∠P=46°(已知),
∴∠AOB=180°-∠P=134°(四边形的内角和定理),
∴∠ACB=
 ∠AOB=72°(同弧所对的圆周角是所对的圆心角的一半).
∠AOB=72°(同弧所对的圆周角是所对的圆心角的一半).故答案是:72°.
点评:综合运用了切线的性质定理、四边形的内角和定理以及圆周角定理.连接OA与OB,熟练运用性质及定理是解本题的关键.

练习册系列答案
相关题目
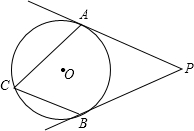 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
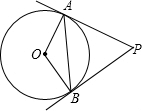 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于