题目内容
如图,直线y=-| 3 |
| 4 |
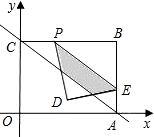 相交于B点,P为BC边上一动点.
相交于B点,P为BC边上一动点.(1)求C点的坐标;
(2)点P从点C出发沿着CB以每秒1个单位长度的速度向点B匀速运动,过点P作PE∥AC交AB于B,设运动时间为t秒,用含t的代数式表示△PBE的面积S;
(3)在(2)的条件下点P的运动过程中,将△PBE沿着PE折叠(如图所示),点B在平面内的落点为点D.当△PDE与△ABC重叠部分的面积等于
| 3 |
| 2 |
分析:(1)结合图形,根据直线y=-
x+6与x轴、y轴分别相交于A、C两点很容易求出点C的坐标.
(2)容易得出四边形OABC是矩形,根据性质得出BP的表达式,因为△BPE∽△BCA,求出BE表达式,进而求出△PBE的面积S.
(3)先求出D点在AC上的特殊位置时t的值,然后分两种情况求解.
| 3 |
| 4 |
(2)容易得出四边形OABC是矩形,根据性质得出BP的表达式,因为△BPE∽△BCA,求出BE表达式,进而求出△PBE的面积S.
(3)先求出D点在AC上的特殊位置时t的值,然后分两种情况求解.
解答: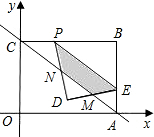 解:(1)当x=0时,y=6
解:(1)当x=0时,y=6
∴点C的坐标为(0,6);
(2)y=-
x+6与x轴相交于点A(8,0)
∵∠AOC=90°,BA⊥OA,BC⊥OC
∴四边形OABC是矩形
∴BC=OA=8,AB=OC=6
∴BP=8-CP=8-t
∵PE∥AC
∴△BPE∽△BCA
∴
=
∴BE=
(8-t)
∴S△PBE=
BP•BE=
(t-8)2=
t2-6t+24;
(3)设PD、DE与AC分别相交于点N、M,得,DP=BP=8-t,DE=BE=
(8-t)
∵PE∥AC
∴∠CNP=∠DPE,∠BPE=∠BCA
又∵∠BPE=∠DPE
∴∠CNP=∠PCN
∴PN=CP
∴当点P为CB的中点时,t=PN=CP=4,点D恰好落在CA上
①当0<t≤4时,PN=CP=tDN=DP-t=8-2t
∵MN∥PE
∴
=
∴DM=
(4-t)
∴S阴影=S△BPE-S△DMN=(
t2-6t+24)-
(4-t)2=
解得t1=
,t2=
>4(舍去)
∴P点的坐标为(
,6)
②当4<t<8时,S阴影=S△BPE=
t2-6t+24=
解得t3=6,t4=10>8(舍去)
∴P点的坐标为(6,6)
即:当重叠部分的面积等于
时,P点的坐标为(
,6)或(6,6)
 解:(1)当x=0时,y=6
解:(1)当x=0时,y=6∴点C的坐标为(0,6);
(2)y=-
| 3 |
| 4 |
∵∠AOC=90°,BA⊥OA,BC⊥OC
∴四边形OABC是矩形
∴BC=OA=8,AB=OC=6
∴BP=8-CP=8-t
∵PE∥AC
∴△BPE∽△BCA
∴
| BP |
| BC |
| BE |
| AB |
∴BE=
| 3 |
| 4 |
∴S△PBE=
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
(3)设PD、DE与AC分别相交于点N、M,得,DP=BP=8-t,DE=BE=
| 3 |
| 4 |
∵PE∥AC
∴∠CNP=∠DPE,∠BPE=∠BCA
又∵∠BPE=∠DPE
∴∠CNP=∠PCN
∴PN=CP
∴当点P为CB的中点时,t=PN=CP=4,点D恰好落在CA上
①当0<t≤4时,PN=CP=tDN=DP-t=8-2t
∵MN∥PE
∴
| DN |
| DP |
| DM |
| DE |
∴DM=
| 3 |
| 2 |
∴S阴影=S△BPE-S△DMN=(
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
解得t1=
8-2
| ||
| 3 |
8+2
| ||
| 3 |
∴P点的坐标为(
8-2
| ||
| 3 |
②当4<t<8时,S阴影=S△BPE=
| 3 |
| 8 |
| 3 |
| 2 |
解得t3=6,t4=10>8(舍去)
∴P点的坐标为(6,6)
即:当重叠部分的面积等于
| 3 |
| 2 |
8-2
| ||
| 3 |
点评:在图形中渗透运动的观点是中考中经常出现的问题,注意理解其具体的意义,画出图形会比较清楚;很多题应该注意情况不止一种以及根的取舍问题,比如说不在定义域内等,联系实际借助图形的帮助更深的理解.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
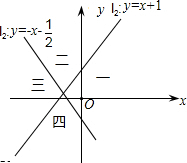 如图,直线l1:y=x+1与直线l2:y=-x-
如图,直线l1:y=x+1与直线l2:y=-x-| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| A、第一部分 | B、第二部分 |
| C、第三部分 | D、第四部分 |
 14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=
14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=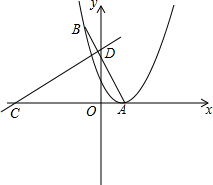 (2012•江汉区模拟)已知:抛物线
(2012•江汉区模拟)已知:抛物线 (2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
(2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是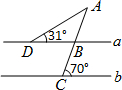 (2012•广州模拟)如图,直线a∥b,则∠A的度数是( )
(2012•广州模拟)如图,直线a∥b,则∠A的度数是( )