题目内容
1.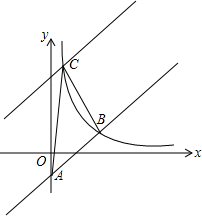 如图,在平面直角坐标系中,直线y=x-2与y轴相交于点A,与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点B(m,2).
如图,在平面直角坐标系中,直线y=x-2与y轴相交于点A,与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点B(m,2).(1)试写出点A的坐标,点A(0,-2 );
(2)求反比例函数的关系式;
(3)将直线y=x-2向上平移后与该反比例函数的图象在第一象限内交于点C,且△ABC的面积为8,求平移后直线的函数表达式.
分析 (1)在y=x-2中令x=0可求得点坐标;
(2)可先求得B点坐标,再代入反比例函数解析式,可求得反比例函数解析式;
(3)过点C作CE⊥y轴,垂足为E,过点B作y轴的垂线,垂足分别为F,连接CF,用x和y表示出△ABC的面积,结合平移的性质可求得平移后的直线的解析式.
解答 解:(1)在y=x-2中,令x=0可得y=-2,
∴A点坐标为(0,-2),
故答案为:0;-2;
(2)∵点B(m,2)在直线y=x-2的图象上,
∴m=4∴B(4,2)
∵点B在反比例函数y=$\frac{k}{x}$的图象上,
∴k=4×2=8,
∴反比例函数的关系式是y=$\frac{8}{x}$;
(3)如图,过点C作CE⊥y轴,垂足为E,过点B作y轴的垂线,垂足分别为F,连接CF,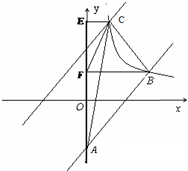
∵S△ABC=S△ABF+S△BCF-S△ACF=$\frac{1}{2}$AF•BF+$\frac{1}{2}$BF•EF-$\frac{1}{2}$CE•AF=$\frac{1}{2}$×4×4+$\frac{1}{2}$×4(y-2)-$\frac{1}{2}$×4x=4-2x+2y,且y=$\frac{8}{x}$,S△ABC=8,
∴4-2x+2×$\frac{8}{x}$=8,即x2+2x-8=0,
∴x=2或x=-4(不合题意,舍去),
∴C(2,4),
∵平移后的直线与直线y=x-2平行,
∴设平移后直线的解析式为:y=x+b,
把点C(2,4)代入得:b=2,
∴y=x+2.
点评 本题主要考查反比例函数和一次函数的交点问题,掌握两函数图象交点的坐标满足每个函数解析式是解题的关键.

练习册系列答案
相关题目
12.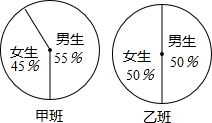 已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
 已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )| A. | 58 | B. | 25 | C. | 27 | D. | 52 |
16.不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其他都相同)其中红球2个,黄球1个,蓝球1个,则搅匀后从中任意摸出一个球是红球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
11.武汉市光谷实验中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),下列说法错误的是( )


| A. | 九(1)班的学生人数为40 | B. | m的值为10 | ||
| C. | n的值为20 | D. | 表示“足球”的扇形的圆心角是70° |
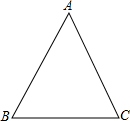 如图,已知△ABC,用尺规作出△ABC的角平分线BD.(保留作图的痕迹,不写作法)
如图,已知△ABC,用尺规作出△ABC的角平分线BD.(保留作图的痕迹,不写作法) 如图,已知C点为线段AB的中点,D点为BC的中点,AB=8cm,求AD的长度.
如图,已知C点为线段AB的中点,D点为BC的中点,AB=8cm,求AD的长度.