题目内容
某游泳爱好者在河中逆流而上,在桥A下面,水壶遗失被水冲走,继续前游20分钟后他发现水壶遗失,于是立即返回追寻水壶,在桥A下游距A,2km的桥B下面追到水壶,求这条河的水流速度.
考点:分式方程的应用
专题:
分析:如果设该河水流的速度是每小时x千米,游泳者在静水中每小时游a千米.那么游泳者自桥A逆流游了
(a-x)千米,他再返回追到水壶用了
小时,这个时间比水壶在遗失后漂流时间
小时少
小时.由此列出方程,求得问题的解.
| 1 |
| 3 |
2+
| ||
| a+x |
| 2 |
| x |
| 1 |
| 3 |
解答:解:设该河水流的速度是每小时x千米,游泳者在静水中每小时游a千米.由题意,得
=
-
,
解得:x=3.
经检验,x=3是原方程的解.
答:这条河的水流速度为3千米/小时.
2+
| ||
| a+x |
| 2 |
| x |
| 1 |
| 3 |
解得:x=3.
经检验,x=3是原方程的解.
答:这条河的水流速度为3千米/小时.
点评:本题考查分式方程的应用.分析题意,找到合适的等量关系是解决问题的关键.本题需注意顺流速度与逆流速度的表示方法.另外,本题求解时设的未知数a,在解方程的过程中抵消.这种方法在解复杂的应用题时常用来帮助分析数量关系,便于解题.

练习册系列答案
相关题目
若3<a<4时,化简|a-3|+|a-4|的结果为( )
| A、2a-7 | B、2a-1 |
| C、1 | D、7 |
 如图:
如图: 如图,Rt△ABO的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A,B两点的坐标分别为(-3,0),(0,4),抛物线y=
如图,Rt△ABO的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A,B两点的坐标分别为(-3,0),(0,4),抛物线y=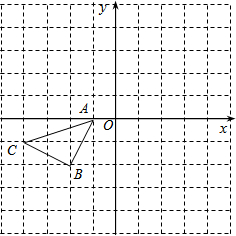 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: